היות ואנו לא יכולים להסביר מדוע משקל הביצים מאותה תרנגולת אינו זהה, מרחק הגלים באותו ים אינו אחיד, ומשקל הכדורים מאותה מכונה אינו שווה, אנו מייחסים זאת לגורם המקריות שקיים בכל תהליך מחזורי.
נתייחס לגורם המקריות תוך שימוש בדוגמת הביצים.
סימולים
M- משקל של ביצה כלשהי (נמדד בגרמים).
– המשקל הממוצע של הביצים (נמדד בגרמים. בדוגמא, 50 גר').
– הפער בין ל – ( ).
מודד לגבי כל ביצה בכמה היא שונה מהמשקל הממוצע. לכן, נמדד בגרמים.
אם משקל הביצה 48 גרם, אז (משקלה קטן ב- 2 גרם מהממוצע).
אם משקל הביצה 51 גרם, אז (משקלה גדול ב- 1 גרם מהממוצע).
אם משקל הביצה 50 גרם, אז (משקלה משתווה לממוצע).
u משתנה מביצה לביצה, ולפיכך הוא משתנה מקרי.
למעשה u מייצג את גורם המקריות של משקל הביצים.
הנחה לגבי התפלגות u
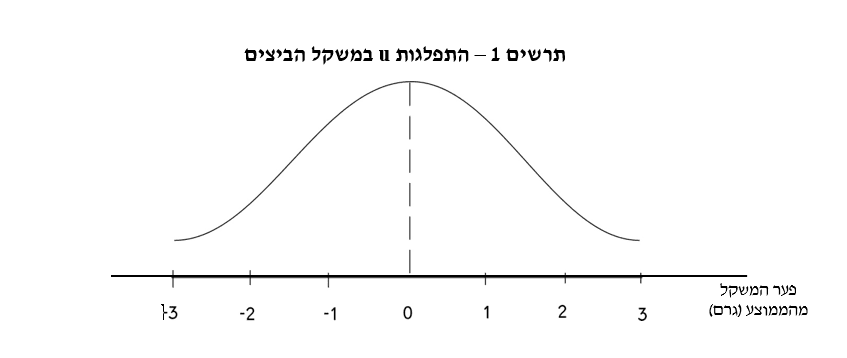
אנו מניחים ש- u מתפלג נורמלית עם תוחלת 0 כפי שמוצג בתרשים 1. תוחלת 0 פרושה
ש- 50% מהביצים שוקלות פחות מהממוצע (u מקבל ערכים שליליים), ו- 50% מהביצים שוקלות יותר מהממוצע (u מקבל ערכים חיוביים).
מלבד התוחלת יש להתפלגות u גם סטיית תקן. אם סטיית התקן היא קטנה, אז הפעמון יהיה גבוה וצר. המשמעות היא שהמשקל של חלק גדול מאוד של הביצים יהיה מאוד קרוב לממוצע (50 גרם). אם סטיית התקן היא גדולה, אז הפעמון יהיה נמוך ורחב. המשמעות היא שיש גם לא מעט ביצים שמשקלן רחוק מ- 50 גרם (גבוה יותר או נמוך יותר).
אנו מסמלים את סטיית התקן של u באות היוונית .
לסיכום, גורם המקריות מתפלג נורמלית עם תוחלת 0, וס”ת כלשהי שנסמלה .
הערה: בכל אחת מהדוגמאות שלעיל (משקל הביצים, המרחק של קו החוף ומשקל כדורי הטניס) יכולה להיות שונה, אבל ההתפלגות תמיד תהיה נורמלית, והתוחלת – תמיד 0.