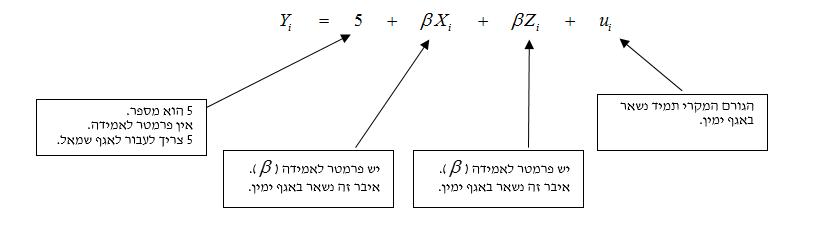
במסגרת מבחן Wald אנו מבצעים מספר מהלכים שבסופם מתקבלת תוצאה שנקראת:
Wald סטטיסטי, שסימולה: .
את ה – Wald הסטטיסטי משווים למספר מסויים שמתקבל מטבלה, המכונה טבלת F (מופיעה בעמוד 58).
אם קטן ממספר זה לא ניתן לדחות את השערת האפס ואנו מחליטים שהמידע המוקדם נכון. אם גדול ממספר זה אנו דוחים את השערת האפס ומחליטים שהמידע המוקדם איננו נכון.
המהלכים לחישוב
- שינוי פני המודל המקורי
- 1. מציבים במודל המקורי את נתוני השערת האפס.
בדוגמה, המודל ישתנה ל: .
- 2. מעבירים לאגף שמאל את כל האיברים שאין בהם פרמטרים לאמידה (הערה: הגורם המקרי תמיד נשאר באגף ימין).
בדוגמה, המצב הוא כדלקמן:
לאחר ההעברה של המספר 5 נקבל:
3. באגף ימין יש לדאוג שכל פרמטר יופיע פעם אחת בלבד, באמצעות הפיכתו לגורם משותף.
בדוגמא, נהפוך את הפרמטר לגורם משותף, ונקבל: .
המודל שהתקבל מכונה המודל המוגבל (Restricted Model).
במודל המוגבל שבדוגמה המשתנה המוסבר הוא , והמשתנה המסביר הוא . נשים לב שהמשתנה המסביר במודל המוגבל הוא סכום של שני משתנים מסבירים במודל המקורי, וכן שבמודל המוגבל אין חותך.
המודל המקורי מכונה המודל הלא-מוגבל (Unrestricted Model) או המודל החופשי.
- ב. אמידה של שני המודלים: המודל הלא-מוגבל (המודל המקורי) והמודל המוגבל
את המודל הלא-מוגבל כבר אמדנו (ראו תרשים 10), אבל יש צורך באמידה המספקת עוד נתונים סטטיסטיים (כמו שעשינו במקרה של ). לשם כך , יש לסמן אזור של 5 שורות, ולקבל תוצאות כמו בתרשים 11.
תרשים 11
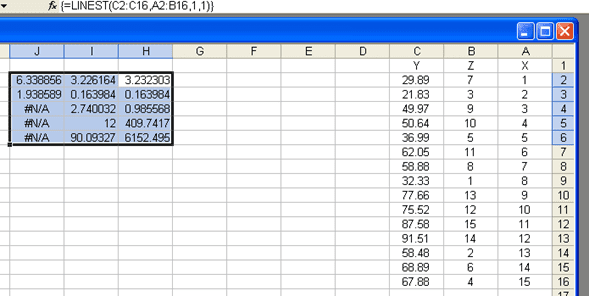
כעת נייצר את המשתנים (המוסבר והמסביר) של המודל המוגבל.
המשתנה המוסבר הוא , והוא מופיע בעמודה F בתרשים 12 (יוצרים אותו ע”י הורדה של המספר 5 מכל ערכי המקוריים המופיעים בעמודה C).
המשתנה המסביר הוא , והוא מופיע בעמודה E בתרשים 12 (יוצרים אותו ע”י סיכום הערכים של ושל המופיעים בעמודות A ו- B).
שימו לב שהאיבר השלישי בפקודת האמידה =LINEST(F2:F16,E2:E16,0,1)
הוא 0, וזאת כדי לציין שבמודל אין חותך.
הערה: תרשים 12 הוא הרחבה של תרשים 11. הוא מכיל הן את האמידה של המודל הלא-מוגבל (כפי שמופיע גם בתרשים 11) והן את האמידה של המודל המוגבל.
תרשים 12
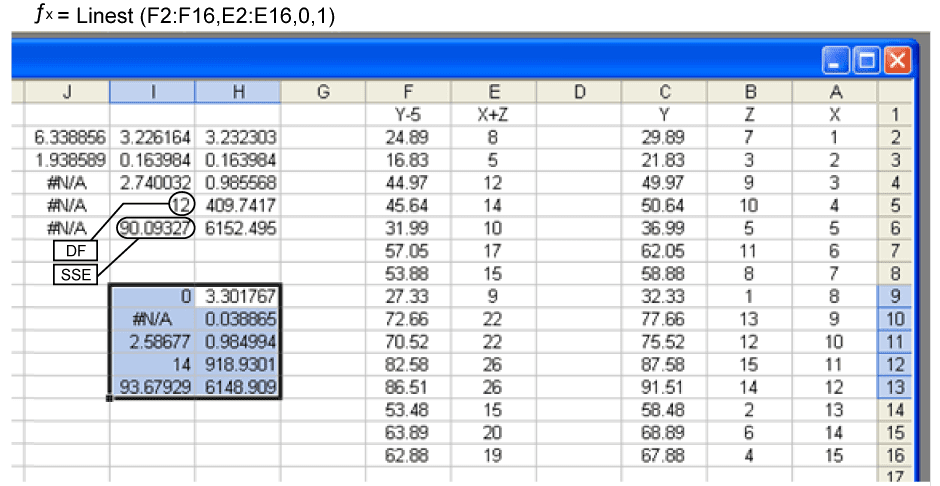
- א. חישוב
לחישוב נתבונן באזור של תוצאות האמידה ונשתמש בתוצאות שנמצאות בשורות הרביעית והחמישית בעמודה השניה (עמודה I).
התוצאה הנמצאת בשורה הרביעית בעמודה השניה משמאל נקראת מספר דרגות החופש וסימולה הוא .
התוצאה הנמצאת בשורה החמישית בעמודה השניה משמאל נקראת סכום ריבועי הסטיות וסימולה הוא .
את התוצאות של המודל הלא-מוגבל נסמן ע”י המילה unrestricted, ואת התוצאות של המודל המוגבל נסמן ע”י המילה restricted.
נשלוף את התוצאות מתוך תרשים 12:
,
,
הנוסחה לחישוב היא:
נציב את נתוני הדוגמא ונקבל:
- א.
- ב.
השוואת עם המספר מתוך טבלת F
נשים לב כי הנוסחה לחישוב בנויה משבר שהן במונה שלו והן במכנה שלו מופיעים שברים. נתבונן במכנים של שברים אלה.
בדוגמא:
- • השבר המופיע במונה של הוא . המכנה של שבר זה הוא 2.
- • השבר המופיע במכנה של הוא . המכנה של שבר זה הוא 12.
שני המכנים הנ”ל 2 ו- 12 יעזרו לנו לשלוף מספר מתוך טבלת F המופיעה כאן.
טבלת F
|
המכנה של המונה |
||||
|
1 |
2 |
3 |
||
|
המכנה של המכנה |
1 |
161 |
200 |
216 |
|
2 |
18.51 |
19.00 |
19.16 |
|
|
3 |
10.13 |
9.55 |
9.28 |
|
|
4 |
7.71 |
6.94 |
6.59 |
|
|
5 |
6.61 |
5.79 |
5.41 |
|
|
6 |
5.99 |
5.14 |
4.76 |
|
|
7 |
5.59 |
4.74 |
4.35 |
|
|
8 |
5.32 |
4.46 |
4.07 |
|
|
9 |
5.12 |
4.26 |
3.86 |
|
|
10 |
4.96 |
4.10 |
3.71 |
|
|
12 |
4.75 |
3.89 |
3.49 |
|
|
15 |
4.54 |
3.68 |
3.29 |
|
|
20 |
4.35 |
3.49 |
3.10 |
|
|
30 |
4.17 |
3.32 |
2.92 |
|
|
60 |
4.00 |
3.15 |
2.76 |
|
|
120 |
3.92 |
3.07 |
2.68 |
|
|
מעל 120 |
3.84 |
3.00 |
2.60 |
נשלוף מתוך הטבלה את המספר המופיע בטור של המכנה של המונה (טור 2) ובשורה של המכנה של המכנה (טור 12). המספר הוא 3.89. מספר זה מכונה הערך הקריטי.
נשווה את (בדוגמה, 0.24) לערך הקריטי (בדוגמה, 3.89).
אם קטן מהערך הקריטי מקבלים את השערת האפס.
אם גדול מהערך הקריטי דוחים את השערת האפס.
בדוגמא, הערך של קטן מהערך הקריטי מהטבלה (). לפיכך איננו דוחים את השערת האפס, ואנו מחליטים כי המידע המוקדם שיש לחוקר
() הוא נכון.