השיטה שבה תוכנת אקסל מחשבת את הערכים של ו- נקראת שיטת הריבועים הפחותים. החישוב נעשה תוך שימוש בנוסחאות שפותחו ע”י מתמטיקאים.
הנוסחאות עצמן נקראות אומדים, והערכים של ו- , המחושבים עפ”י הנוסחאות האלה מהמדגם הספציפי, נקראים אומדנים.
האומדים לפי שיטת הריבועים הפחותים נקראים אומדי הריבועים הפחותים (אר”פ) או אומדי OLS (ראשי תיבות של Ordinary Least Squares).
עבור כל מדגם נשתמש באותה נוסחא כדי לחשב את ו- . כלומר, האומדים לא משתנים ממדגם למדגם (הנוסחאות לא תלויות במדגם).
האומדנים, לעומת זאת, עשויים להשתנות ממדגם למדגם. כלומר, האומדים מניבים ערכים שהם משתנים מקריים כי האומדנים המחושבים לפיהם הם תלויי מדגם. כל מדגם יתן ערך אחר.
לאומדי הריבועים הפחותים שתי תכונות הנחשבות טובות מבחינה סטטיסטית:
- הם חסרי הטיה
- שונותם קטנה יחסית לאומדים בשיטות אחרות.
כדי להסביר שתי תכונות אלה נתבונן במודל . היינו רוצים לדעת את ואת , אבל לא נוכל לדעת אותם אלא רק לאמוד אותם, כלומר לחשב את ואת .
אומדי הריבועים הפחותים הם חסרי הטיה
אם נשתמש באומדי הריבועים הפחותים כדי לחשב את , אזי הסיכוי ש- שנקבל יהיה גדול מ- האמיתי, זהה לסיכוי שהוא יהיה קטן ממנו.
במילים אחרות: מרכז פעמון ההתפלגות של נמצא ב- האמיתי.
אומדי הריבועים הפחותים הם בעלי שונות קטנה יחסית
השונות של אומדי הריבועים הפחותים היא קטנה יחסית. הדבר גורם לכך שהאומדנים המתקבלים במדגמים שונים יהיו מפוזרים ברובם הגדול באזור קטן על ציר המספרים.
נדגים את שתי התכונות האלה בתרשימים, ונראה מדוע הן נחשבות תכונות טובות.
הדגמת התכונות בתרשימים
אם אומד הוא גם חסר הטיה וגם בעל שונות קטנה, אז בסיכוי גבוה האומדן המתקבל ממנו יהיה מדוייק יחסית.
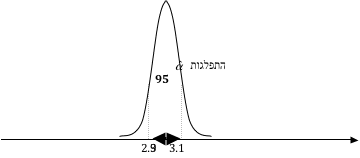
למשל, נניח כי , והאומד שבו אנו משתמשים כדי לחשב את הוא אומד חסר הטיה עם שונות נמוכה. התרשים ממחיש את הדבר:
לפי התרשים, בגלל שהשונות קטנה, ב- 95% מהמקרים שיתקבל יהיה בין 2.9 לבין 3.1. ואם הערך האמיתי הוא 3, הרי שהערך הנאמד הוא לא רחוק ממנו והוא משקף אותו בצורה טובה.
נתבונן כעת במקרה שבו האומד מוטה (לא חסר הטיה), למשל, נניח שמרכז ההתפלגות נמצא ב- 3.5 (ולא ב- 3), והשונות היא כמו בתרשים הקודם.
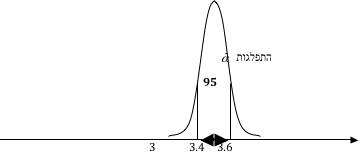
לפי התרשים, ב- 95% מהמקרים שיתקבל יהיה בין 3.4 לבין 3.6. מכיוון שהערך האמיתי הוא 3, הרי שהערך הנאמד רחוק מהערך האמיתי ואיננו משקף אותו בצורה טובה.
נתבונן במקרה שבו האומד חסר הטיה אך בעל שונות גדולה.

לפי התרשים, ב- 95% מהמקרים שיתקבל יהיה בין 0.5 לבין 5.5. מכיוון שהערך האמיתי הוא 3, הרי שהערך הנאמד רחוק מהערך האמיתי ואיננו משקף אותו בצורה טובה.
לסיכום: אומדי הריבועים הפחותים הם חסרי הטיה עם שונות קטנה (כמו בתרשים הראשון), ולכן האומדנים הנובעים מהם ( ו- ) משקפים באופן מדוייק יחסית את הערכים האמיתיים ( ו- ).