כפי שראינו קו ה-CML נותן את תוחלת התשואה של תיקים יעילים, אך לא של מניות בודדות.
מודל ה-CAPM מתמקד בבחירת “תיק השקעות” בשוק ניירות הערך ומציע נוסחה למציאת תוחלת התשואה גם של מניות בודדות.
מיקרא:
- `beta` – הביתא של המניה i הבודדת עם תיק השוק, מנבאת את הסיכון השיטתי הצפוי בעתיד על סמך נתוני העבר.
- `Sigma_(i,m` – שונות משותפת של מניה i עם תיק השוק.
- `Sigma_m^2` – סטיית תקן של תיק השוק בריבוע, כלומר שונות תיק השוק.
מודל ה-CAPM משתמש במדד הביתא β כדי לקבוע את תוחלת התשואה של מניות בודדות, כי לפי המודל רק תנודות בתשואת המניה הבודדת (i), שמתואמות עם התנודות בתשואת תיק השוק, יזכו את המניה בתוספת לתוחלת תשואה שלה. הרעיון הוא שתנודות בתשואת המניה הבודדת i שהן ספציפיות למניה הבודדת, ולא קשורות לתנודות בשוק כולו, לא יזכו בתוספת תשואה למחזיק במניה i.
מדוע? ירידות במחיר המניה שקשורות לפירמה i עצמה ורק לה, ניתנות לפיזור ע”י החזקת תיק השקעות גדול שמפוזר היטב ומכיל מספר רב של מניות (זהו תיק השוק). לכן סיכונים ספציפיים למניה ספציפית לא יזכו בתוספת תשואה. משקיע חכם יפזר היטב את תיק ההשקעה שלו וימנע מסיכונים ספציפיים שלו.
לעומת זאת, מתנודות במחיר המניה הבודדת שמתואמות עם תנודות במחיר תיק השוק כולו, לא ניתן להימנע.
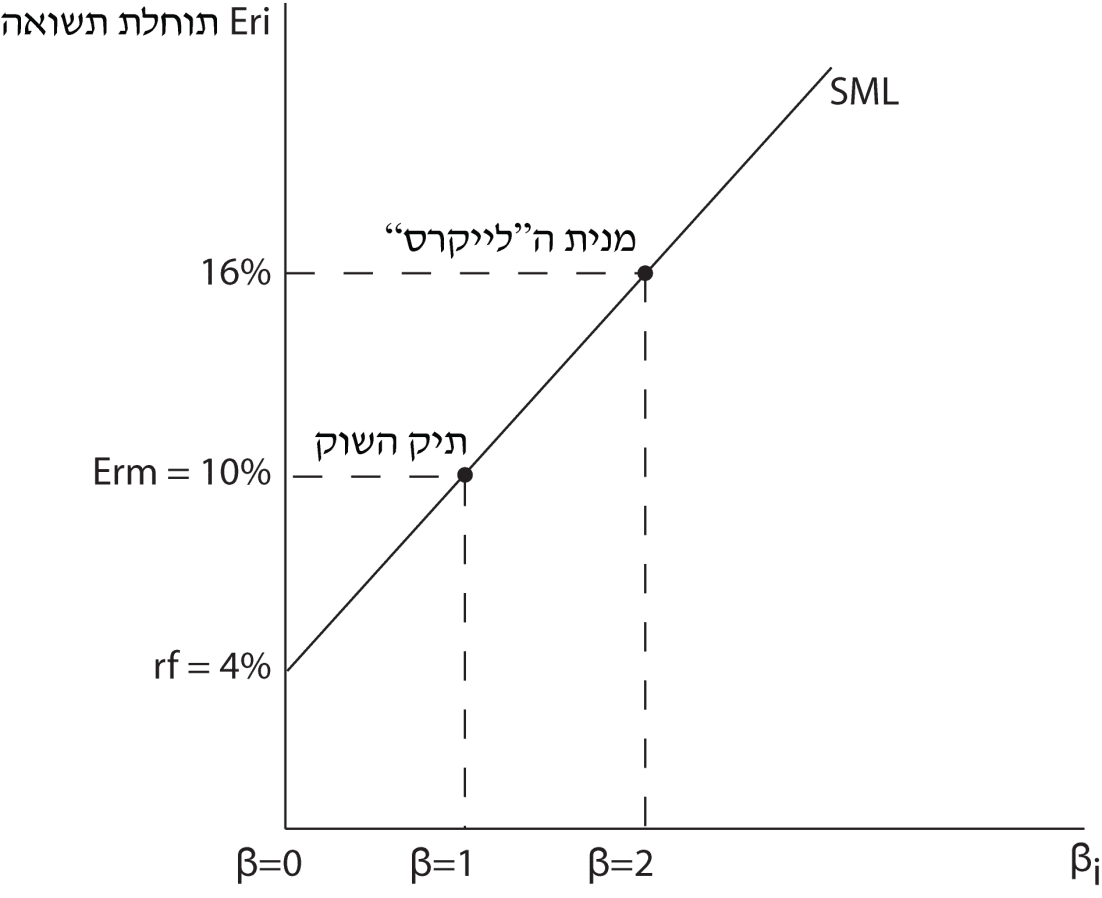
נוסחת ה- SML שנותנת את תוחלת התשואה של מניה בודדת לכל רמת β של מניה היא:
`E_(ri)=rf+beta_i(E_(rm)-rf)`
מה היא הביתא של תיק השוק עצמו?
דוגמה:
מהי תוחלת התשואה על מנית “הלייקרס” לפי מודל ה- CAPM ?
תרשים 21