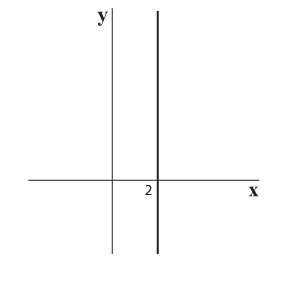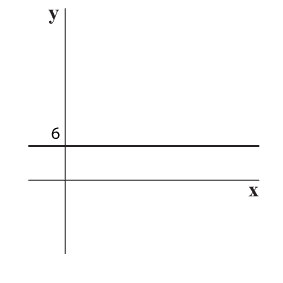לפונקציה בעלת שני משתנים ישנן שתי נגזרות
לפונקציה בעלת שני משתנים ישנן שתי נגזרות. נגזרת לפי x ונגזרת לפי y.
כאשר אנו גוזרים לפי x אנו מייחסים ל-y מספר קבוע כלשהו, למשל 6.
כאשר אנו גוזרים לפי y אנו מייחסים ל-x מספר קבוע כלשהו, למשל 2.
דוגמה א'
נתייחס לפונקציה f(x,y)=4x+5y
- נגזור לפי x. נניח כי 6=y, כך שהפונקציה הופכת להיות f(x)=4x+30. הנגזרת לפי x (על פי כללי הגזירה), היא 4.
- נגזור לפי y. נניח כי 2=x, כך שהפונקציה הופכת להיות f(y)=8+5y. הנגזרת לפי y היא 5.
סימולים
נגזרת לפי x: fx(x,y)
נגזרת לפי y: fy(x,y)
בדוגמה א' לעיל, תוצאות הנגזרת תרשמנה כך:
fx(x,y)=4
fy(x,y)=5
המשמעות ש- y הוא מספר קבוע כלשהו (למשל – 6)
ההסבר מתייחס לפונקציה f(x,y)=4x+5y בדוגמה א'.
כאשר y הוא מספר קבוע כלשהו, למשל 6, אזי אנו למעשה משאירים מהמעטפת של הפונקציה רק רצועה אחת ברוחב מיקרוסקופי שמיקומה מעל קו רוחב 6. כל שאר המעטפת נעלמת. לרצועה שמעל קו רוחב 6 נקרא: רצועת רוחב 6.
רצועת רוחב 6 היא למעשה פונקציה שטוחה (דו מימדית) במישור הצירים x ו- z. במילים אחרות, רצועת רוחב 6 היא פונקציה של x שסימולה ומרכיביה הם: f(x)=4x+30.
כאשר אנו גוזרים את רצועת רוחב 6 אנו למעשה מקבלים פונקציה (=פונקציית הנגזרת), שבאמצעותה אנו יכולים לחשב את השיפוע בכל נקודה על רצועת רוחב 6.
התרשים הבא מציג את רצועת רוחב 6 משתי נקודות מבט: 1. מלמעלה 2. מלפנים.
מבט מלמעלה
במבט מלמעלה הרצועה נראית כקו ישר המתלכד עם רצועת רוחב 6.
התוואי הוא פונקציה של x .
מבט מלפנים (מציר ה x)
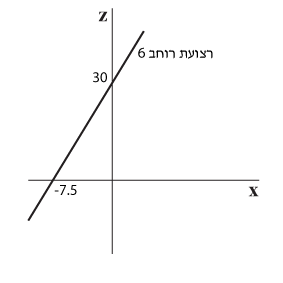
במבט מלפנים (מציר ה- x) אנו רואים את תוואי הרצועה במישור x-z.
המשמעות ש- x הוא מספר קבוע כלשהו (למשל – 2)
כאשר x הוא מספר קבוע כלשהו, למשל 2, אזי אנו למעשה משאירים מהמעטפת של הפונקציה רק רצועה אחת ברוחב מיקרוסקופי שמיקומה מעל קו אורך 2.
כל שאר המעטפת נעלמת.
לרצועה שמעל קו אורך 2 נקרא: רצועת אורך 2.
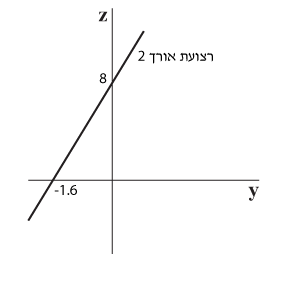
רצועת אורך 2 היא למעשה פונקציה “שטוחה” במישור הצירים y ו- z, שסימולה ומרכיביה הם: f(y)=8+5y.
שימו לב:
על רצועת רוחב אנו מתבוננים מציר ה- x (כשמתבוננים מלפנים).
על רצועת אורך אנו מתבוננים מציר ה- y (כשמתבוננים מלפנים).
כאשר אנו גוזרים את רצועת אורך 2, אנו מקבלים למעשה פונקציה (=פונקציית הנגזרת), שבאמצעותה אנו יכולים לחשב את השיפוע בכל נקודה על הרצועה.
התרשים הבא מציג את רצועת אורך 2 משתי נקודות מבט:
- מלמעלה
- מלפנים (מציר ה- y).
המבט מלפנים על רצועות אורך הוא מציר ה- y.
מבט מלמעלה
