התייחסות למין של העובדים
כאשר הסטודנט יחקור את המין של העובדים הוא יערוך טבלה כדוגמת הטבלה הבאה:
|
1 |
2 |
3 |
|
הערך |
השכיחות (מספר העובדים) |
השכיחות היחסית (ב-%, מעוגל) |
|
גבר |
8 |
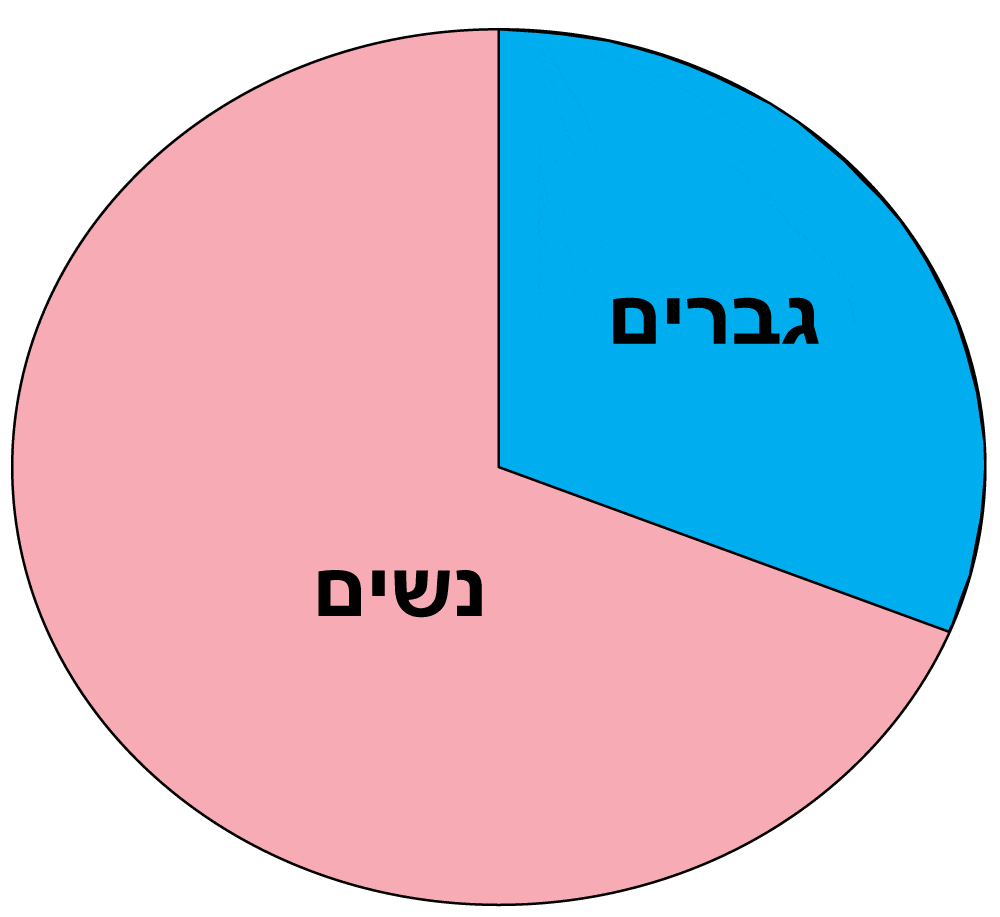
27% |
|
אשה |
22 |
73% |
|
סה”כ |
30 |
100% |
בטבלה זו המין הוא המשתנה הנחקר. מדוע משתנה? מכיוון שהמין הוא תכונה שאיננה קבועה אצל כל העובדים אלא משתנה מעובד לעובד. עובד יכול להיות “גבר” או “אשה”, או בשפה מקצועית יותר: משתנה המין יכול לקבל שני ערכים: “גבר” ו – “אשה”.
הטבלה שלעיל נקראת טבלת שכיחויות. יש בה שלושה טורים:
- בטור הראשון מופיעים הערכים שיכול לקבל המשתנה הנחקר: “גבר” או “אשה”.
- בטור השני תופיע השכיחות של כל ערך: מול הערך “גבר” יופיע מספר הגברים במשרד ומול הערך “אשה” יופיע מספר הנשים במשרד.
- בטור השלישי תופיע השכיחות היחסית של כל ערך באחוזים: בשורה של הגברים יופיע אחוז הגברים מכלל העובדים במשרד, ובשורה של הנשים יופיע אחוז הנשים מכלל העובדים במשרד.
לפי טבלה זו במשרד עובדים 8 גברים והם מהווים 27% מכלל העובדים במשרד. מספרן של הנשים גדול יותר, 22, והן מהוות 73% מכלל העובדים במשרד.
בטבלת שכיחויות נהוג להוסיף שורה נוספת (השורה האחרונה) שבה יופיעו הסיכומים של הטורים.
נעיר כי במקרה של המין אין חשיבות לסדר הרישום בטבלה והסטודנט היה יכול לכתוב את הנשים בשורה הראשונה ואת הגברים בשניה.
את טבלת השכיחויות ניתן להציג באופן ויזואלי באמצעות דיאגרמת עוגה:
הדיאגרמה נקראת דיאגרמת עוגה על שום צורתה העגולה. כל ערך (נשים או גברים) מקבל שטח בעוגה לפי השכיחות היחסית שלו. במקרה שלנו הגברים מקבלים 27% מהשטח (ואכן רואים שהגברים מקבלים קצת יותר מרבע עוגה) והנשים מקבלות את 73% הנותרים.
הדיאגרמה והטבלאות עונות לנו על השאלה: מהי ההתפלגות של המין בקרב עובדי המשרד? ההתפלגות היא האופן שבו מתחלקים עובדי המשרד לגברים ונשים. במשרד אחר, למשל, היתה יכולה להיות התפלגות אחרת.
התייחסות למצב המשפחתי של העובדים
אותו תהליך של ארגון נתונים ניתן לעשות גם על סעיף המצב המשפחתי. כלומר, לבדוק את ההתפלגות של המצב המשפחתי בקרב עובדי המשרד. גם המצב המשפחתי הוא משתנה שבו אין חשיבות לסדר. משתנה המצב המשפחתי יכול לקבל את הערכים “גרוש”, “נשוי”, “רווק” ו”אלמן”, כאשר הסדר ביניהם איננו חשוב. לפיכך, נבנה טבלת שכיחויות באופן הבא:
- בטור הראשון נכתוב את הערכים הנ”ל (גרוש, נשוי,רווק,אלמן) בכל סדר שנחפוץ – זהו טור הערך.
- בטור השני נכתוב עבור כל ערך את השכיחות שלו (מספר העובדים) – זהו טור השכיחות.
- נחשב עבור כל ערך את החלק שהוא מהווה מכלל כמות הנתונים.
- בטור השלישי נכתוב בו את תוצאות החישוב של סעיף (3) – זהו טור השכיחות היחסית.
שני הטורים הראשונים:
|
1 |
2 |
|
הערך (המצב המשפחתי) |
השכיחות |
|
רווק/רווקה |
6 |
|
אלמן/אלמנה |
1 |
|
גרוש/גרושה |
4 |
|
נשוי/נשואה |
19 |
|
סה”כ |
30 |
חישוב השכיחויות היחסיות:
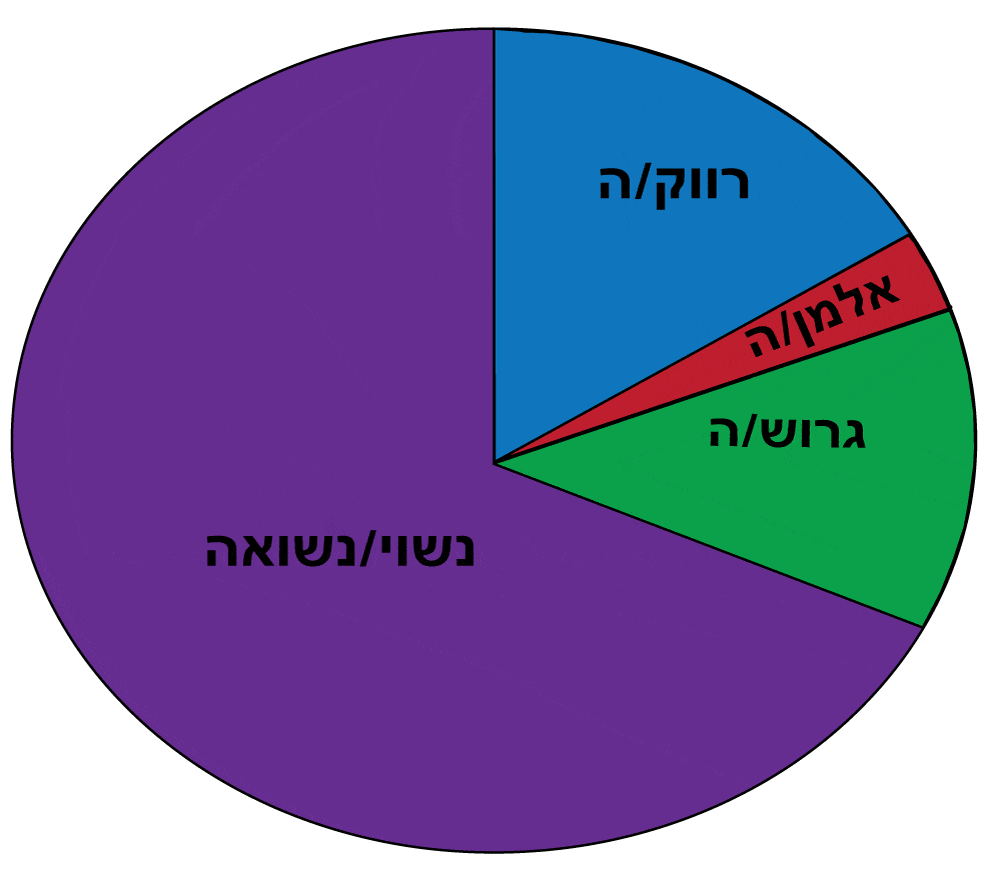
עבור רווק/רווק: `(6)/(30) = 20.00%`
עבור אלמן/אלמנה: `(1)/(30) = 3.33%`
עבור גרוש/גרושה: `(4)/(30) = 13.33%`
עבור נשוי/נשואה: `(19)/(30) = 63.33%`
עבור הקבוצה האחרונה (נשוי/נשואה) ניתן לחשב גם באמצעות השלמה ל – 100%: סכום ולמצוא את האחוזים של כל הקבוצות הראשונות הוא ולכן כדי להשלים
ל – 100% האחוזים של הקבוצה האחרונה יש לחסר .
בשל בעיות עיגול מספרים יש הבדל קטן בין שני החישובים: בראשון קיבלנו 63.33% ובשני 63.34%. אנחנו נעדיף את השני כדי שכל השכיחויות היחסיות יסתכמו ל – 100% בדיוק.
כעת נוסיף את החישובים כטור שלישי בטבלה ונקבל את טבלת השכיחויות:
|
1 |
2 |
3 |
|
הערך (המצב המשפחתי) |
השכיחות |
השכיחות היחסית |
|
רווק/ה |
6 |
20.00% |
|
אלמן/אלמנה |
1 |
3.33% |
|
גרוש/ה |
4 |
13.33% |
|
נשוי/נשואה |
19 |
63.34% |
|
סה”כ |
30 |
100.00% |
לאחר שאירגנו את הנתונים בטבלה נוכל לייצג את ההתפלגות של המצב המשפחתי באמצעות דיאגרמת עוגה. הפעם יהיו בעוגה 4 “פרוסות”: