שאלה 1
ידוע כי מספר התפוזים על העצים בפרדס א' מתפלג נורמלית עם תוחלת 100 (סטיית התקן לא ידועה). בעקבות שימוש בזבל חדש הועלתה הטענה כי מספר התפוזים על העצים גדל. לשם בדיקת הטענה נערך מדגם על תשעה עצים. מספר התפוזים על עצי המדגם היו כדקלמן: 110,108,115,109,105,117,111,110,108. יש לבדוק את הטענה ברמת מובהקות של 5%.
מהלכי הפתרון
- הגדרת השערת ה-0 – הזבל לא יעיל (התוחלת היא 100).
- הגדרת ההשערה הנגדית – הזבל יעיל (התוחלת גדולה מ-100). יהיה קו אדום אחד מימין ל-100.
- יש קו אדום אחד, רמת מובהקות היא 5%, מספר דרגות החופש הוא 8 (גודל המדגם פחות 1).
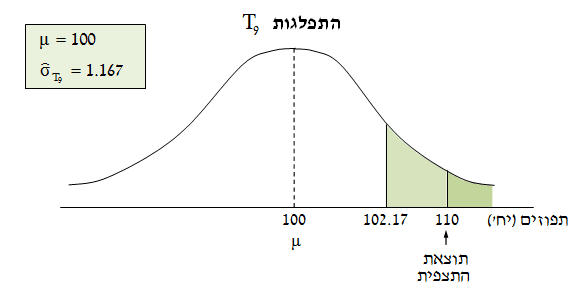
הערך המתאים מטבלה t הוא 1.86. - ממוצע המדגם הוא 110 תפוזים. (וודאו את החישוב)
- טעות התקן של משתנה הבסיס, T1, היא 3.5 תפוזים. (וודאו את החישוב)
- טעות התקן של משתנה הממוצע, T9, היא 1.167 תפוזים `[3.5/sqrt(9)=1.167]`
- הקו האדום יקבע בערך של 102.17 תפוזים `(102.17=1.167*1.86+100)` .
- המסקנה הסטטיסטית היא שההשערה הנגדית מתקבלת (הזבל יעיל), כי הממוצע נמצא בתחום החריג.
שאלה 2
ממחקרים שנעשו בעבר ידוע כי מספר הגרעינים במלון מתפלג נורמלית עם תוחלת 200 (סטיית התקן לא ידועה). חוקר טוען כי עקב התחממות כדור הארץ, השתנה מספר זה והוא איננו 200. לצורך כך הוא ערך מדגם בן 36 מלונים וספר את מספר הגרעינים בכל מלון. הוא חישב את הממוצע ומצא כי הוא 210. לאחר שמצא את הממוצע הוא חישב את סטיית התקן המוערכת (שהיא טעות התקן) של משתנה הבסיס ומצא שהיא 54 גרעינים. האם לפי תוצאות המדגם טענת החוקר נכונה ברמת מובהקות של 5%?
מהלכי הפתרון
- הגדרת השערת ה-0 – ההתחממות לא משפיעה על מספר הגרעינים (התוחלת היא 200).
- הגדרת ההשערה הנגדית – ההתחממות משפיעה על מספר הגרעינים (התוחלת שונה מ-100).
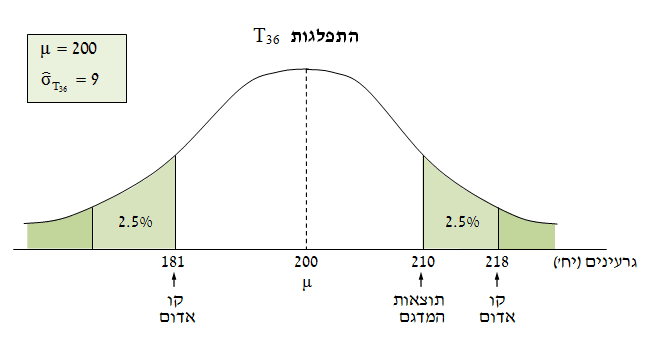
יהיו שני קווים אדומים אחד מימין ל-200 ואחד משמאל ל-200. - יש שני קווים אדומים אחד, רמת מובהקות היא 5%, מספר דרגות החופש הוא 35 (גודל המדגם פחות 1).
הערך המתאים אינו מופיע בטבלה t הנתונה בספר זה, לכן נשתמש בערך המתאים ל-30 דרגות חופש, כלומר 2.042. - ממוצע המדגם הוא 210 גרעינים. (נתון בשאלה)
- טעות התקן של משתנה הבסיס, T1, היא 54 גרעינים. (נתון בשאלה)
- טעות התקן של משתנה הממוצע, T36, היא 9 גרעינים `[54/sqrt(36)=9]`
- הקווים האדומים יקבעו בערכים הבאים:
`218.38=2.042*9+200`
`181.62=2.042*9-200` - המסקנה הסטטיסטית היא שהשערת ה-0 מתקבלת (המספר הגרעינים לא השתנה בעקבות הההתחממות), כי הממוצע נמצא בתחום הסביר.
שאלה 3
ידוע שהטמפרטורה בת”א ביום קיץ (מתחילת יוני ועד סוף ספטמבר) מתפלגת נורמלית. מטאורולוג מדד את הטמפרטורה ב- 9 ימים בקיץ וקיבל את המדגם הבא: 26 (מעלות), 30, 32, 27, 30, 28, 35, 29, 33.
מצא את הרווח סמך לתוחלת הטמפרטורה ברמת סמך של 95%.
מהלכי הפתרון
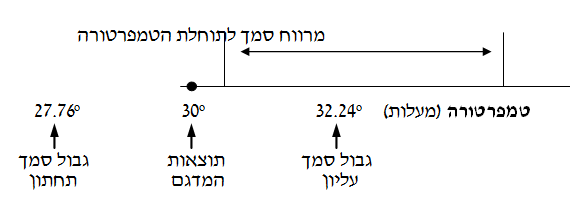
- ממוצע המדגם הוא 300
- רמת הסמך היא 95%, מספר דרגות החופש הוא 8 (גודל המדגם פחות 1). הערך המתאים מטבלה t הוא 2.306.
- טעות התקן של משתנה הבסיס, T1 , היא 2.9150
- טעות התקן של משתנה הממוצע, T9, היא 0.9720
- הגבול העליון של מרווח הסמך הוא `32.24=0.972*2.306+30`
- הגבול התחתון של מרווח הסמך הוא `27.76=0.972*2.306-30`
שאלה 4
מהלכי הפתרון
נסמל את משתנה הבסיס (משקל של ביצה אחת) ב- B1.
נסמל את משתנה הממוצע (משקל ממוצע של ביצה במדגם של 16 ביצים) ב- B16.
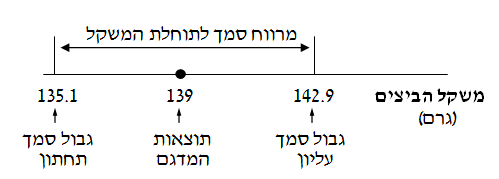
- ממוצע המדגם הוא 139 גרם
- רמת הסמך היא 90%, מספר דרגות החופש הוא 15 (גודל המדגם פחות 1).
הערך המתאים לא מופיע בטבלה t, נשתמש בערך המתאים ל-13 דרגות חופש, שהוא 1.771. - טעות התקן של משתנה הבסיס, B1, היא 8.892 גרם
- טעות התקן של משתנה הממוצע, B16, היא 2.223 גרם
- הגבול העליון של מרווח הסמך הוא `142.9=2.223*1.771+139`
- הגבול התחתון של מרווח הסמך הוא `135.1=2.223*1.771-139`