מגבלת התקציב נותנת ביטוי לאפשרויות הצריכה של גורמי הייצור בפירמה בעלת תקציב מוגבל.
בדוגמא להלן נתייחס לפירמת “המרהט” שצורכת רק שני גורמי ייצור:
- עובדים שעלותם 200 ש”ח לעובד ליום.
- מכונות שעלותן 100 ש”ח למכונה ליום (עלות ליסינג).
תקציב הפירמה הוא 1000 ש”ח ליום.
מדי יום הפירמה יכולה להפעיל בתקציבה הרכבים שונים משני גורמי הייצור, למשל:
3 עובדים ו-4 מכונות.
לכל הרכב של שני גורמי ייצור נקרא: סל גורמי ייצור, ובקיצור: סל.
משוואת מגבלת התקציב של “המרהט”
את המגבלה של כמות גורמי הייצור שניתן להפעיל תמורת 1000 ש”ח ליום, ניתן להציג באמצעות משוואה 1.
משוואה 1: `1000=200X+100y`
- `x` – מסמל את כמות העובדים.
- `y ` – מסמל את כמות המכונות.
אם נבודד את y נקבל את משוואה 2.
משוואה 2:
`y=[(1000-200x)/100]=10-2x`
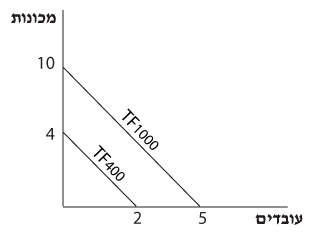
תרשים 2.3
משוואה 2 מציגה את y כפונקציה של x.
`TF ` – תקציב הפירמה
מיקום הסל הנבחר
נתייחס למיקום הסל הנבחר בשני תרחישים, המתייחסים לסדר העדיפות של הפירמה.
תרחיש 1: הפירמה קבעה לעצמה כמות ייצור כלשהי, שנקרא לה: כמות המטרה (ותקציב גורמי הייצור נגזר בהתאם לכך).
תרחיש 2: הפירמה קבעה לעצמה תקציב כלשהו לגורמי הייצור, שנקרא לו: תקציב המטרה (וכמות הייצור נגזרת בהתאם לכך).
תרחיש 1: הפירמה קבעה “כמות מטרה” (לדוגמא 100 יח')- תרשים 2.4
בתרחיש זה הסל הנבחר אמור להימצא בעקומת שוות תפוקה המתייחסת לכמות המטרה
`P_100` , ומקומו המדויק של הסל הנבחר ייקבע במקום ההשקה שלה, עם קו תקציב כלשהו.
וההסבר: אין סל זול ממנו להפקת כמות המטרה.
בכל קו תקציב מתחתיו, אין אפשרות לייצר את כמות המטרה ובכל קו תקציב מעליו ניתן כבר לייצר יותר מכמות המטרה.
תרשים 2.4
משוואה כללית למגבלת התקציב
המשוואה מתייחסת לשני גורמי ייצור: גורם ייצור x וגורם ייצור y.
המגבלה לגבי כמות גורמי הייצור שהפירמה יכולה לרכוש בתקציבה מוצגת באמצעות משוואה 1.
משוואה 1:
`TF=x*P_(x)+y*P_(y)`
נבודד את y ונקבל את משוואה 2:
`y=[(TF-x*P_(x))/P_(y)]=(TF)/P_(y)-P_(x)/P_(y)*x`
משוואה 2 מציגה את y כפונקציה של x.
לפונקציה זו מקובל לקרוא פונקציית מגבלת התקציב (של הפירמה).
ובקיצור: פונקציית התקציב.
מאפייני פונקציית התקציב
- צורתה– קו ישר
- שיפועה – `-P_(x)/P_(y)`
- חיתוך עם ציר y – בערך `(TF)/P_(y)`
- חיתוך עם ציר x – בערך `(TF)/P_(x)`
הצגה גרפית של פונקציית התקציב
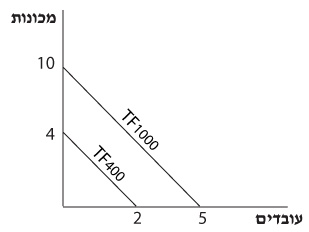
תרשים 2.5 מציג את תוואי הפונקציה.
תרשים 2.5
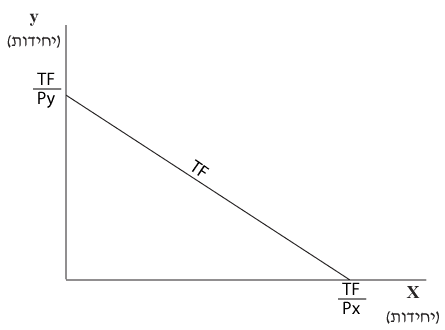
מערכת צירים
- ציר `x` – מתייחס לכמויות מגורם ייצור x שהסל מכיל.
- ציר `y` – מתייחס לכמויות מגורם ייצור y שהסל מכיל.
קו מגבלת התקציב
לקטע שעובר בערכים החיוביים של `x` ו- `y` קוראים: מגבלת התקציב ובקיצור: קו התקציב.
קו התקציב הוא הקטע הרלוונטי עבורנו בפונקציה.
כל נקודה על קו התקציב מייצגת סל שעלותו שווה לתקציב הפירמה (`TF` ).
לכל נקודה בתרשים 2.5 נקרא מדי פעם גם סל.
ניתן להתייחס לכל סל באמצעות נקודת הציון שלו במישור הצירים.
סימול קו מגבלת התקציב
את קו מגבלת התקציב מקובל לסמן ב- `TF` .
אם ידוע סכום התקציב ואנו מעוניינים לציין, מוסיפים את הסכום מימין.
לדוגמא: קו מגבלת התקציב של “המרהט” יסומל ב- `TF_1000` .
קו מגבלת התקציב של “המרהט”
קו מגבלת התקציב של “המרהט” מתבסס על משוואת קו התקציב שלה שצורתה `y=10-2x`
שיפוע הקו הוא 2.
- נקודת החיתוך עם ציר` y` היא 10 (נקודה A).
- נקודת החיתוך עם ציר `x` היא 5 (נקודה B).
במסגרת כל אחד מהסלים שעל קו מגבלת התקציב, אם “המרהט” ירצה להוסיף עובד, יהיה עליו לוותר על 2 מכונות (בהתאם לשיפוע).
תרשים 2.6

מחירי השוק
- `TF` – 1000 ש”ח
- `P_x ` – 200 ש”ח
- `P_y` – 100 ש”ח
כיצד לשרטט את קו התקציב
יש למצוא את נקודות המפגש של קו התקציב עם הצירים ולהעביר קו ביניהן:
- נקודת המפגש עם ציר `y` (סל A) היא `(TF)/P_(y)`
- נקודת המפגש עם ציר `x` (סל B) היא `(TF)/P_(x)`
תרחיש 2 : הפירמה קבעה “תקציב מטרה” (לדוגמא `TF_400` )- תרשים 2.7
כאשר התקציב נתון הסל המועדף יהיה בְמַקוֹם שעקומה שוות תפוקה כלשהי, משיקה לו. בתרשים 2.7 עקומה שוות התפוקה `P_200` משיקה לו והפירמה מייצרת 200 יחידות.
וההסבר: בכל סל אחר על `TF_400` , כמות הייצור תהיה קטנה מ -200 יח' .
תרשים 2.7