את הסינרגיה בין גורמי הייצור מקובל למיין במסגרת 3 קטגוריות:

  • מסייעים (זה לזה)
  • יריבים (זה לזה)
  • בלתי תלויים (זה בזה)

טכניקת המיון מתבצעת באמצעות הנגזרת הצולבת – כלומר, נגזרת שניה לפי K כשהנגזרת הראשונה היא לפי `[X_(LK)]`,או להיפך, כלומר `[X_(KL)]`.

הנגזרות הצולבות` X_(LK`  ו- `X_(KL`  שוות זו לזו, ולכן לא משנה באיזו מהן נשתמש.

  • כאשר  `X_(LK)>0`  גורמי הייצור  מסייעים
  • כאשר  `X_(LK)<0`  גורמי הייצור יריבים
  • כאשר `X_(LK)=0` גורמי הייצור בלתי תלויים

 

פרשנות
`X_L`  היא התפוקה השולית של עובדים.
`X_(LK`  מציג את ההשפעה על התפוקה כאשר בד בבד עם הגידול במספר העובדים גדל גם מספר המכונות.
כאשר `X_(LK`  חיובי, המשמעות היא: תוספת מכונות בד בבד עם הגידול בעובדים, גורמת לגידול בתפוקה.
כאשר `X_(LK`  שלילי, המשמעות היא: תוספת מכונות בד בבד עם הגידול בעובדים, גורמת לקיטון בתפוקה.
כאשר`X_(LK`  = 0, המשמעות היא: תוספת מכונות בד בבד עם הגידול בעובדים, לא משפיעה על תפוקת העובדים.

 

דוגמאות

דוגמא 1

נבחן את הסינרגיה בין גורמי הייצור כאשר פונקציית הייצור היא `x=L*K` .
ההבחנה נעשית בהתאם לתוצאת `X_(LK` .
`K_L=K`
`X_(LK)=1>0` 
המסקנה: גורמי הייצור מסייעים.

 

דוגמא 2

נבחן את הסינרגיה בין גורמי הייצור כאשר פונקציית הייצור היא `X=L^alpha*K^beta` ,
`alphagt0` , `betagt0` .
`K_L=alphaL^(alpha-1)*K^beta`
`X_(LK)=alphaL^(alpha-1)*betaK^(beta-1)`
התוצאה: `X_(LK)gt0` , שכן כל הנתונים בנגזרת השנייה חיוביים (α, β, L ו-K). 
`K^(beta-1)` ו- `L^(alpha-1)` יכולים להיות גם שבר, אך תמיד שבר חיובי.
המסקנה: גורמי הייצור מסייעים.

 

דוגמא 3

פונקציית הייצור היא `x=3L+5K`
`X_L=3`
`X_(LK)=0`
המסקנה: גורמי הייצור בלתי תלויים.

 

קווי תקציב (עקומות שוות עלות)

כל הסלים שמחירם זהה מקיימים את המשוואה `I=L*P_L+K*P_K` .
אם נבודד את K נקבל את משוואה 1:
משוואה 1: `K+I/P_K-P_L/P_(K)L` 

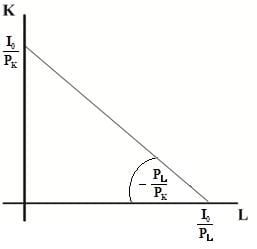
ע”פ תרשים 2, משוואה 1 מייצגת קו ישר שמאפייניו:

  • נקודת החיתוך עם הציר האנכי:  `I/P_K`
  • שיפועו:   `-P_L/P_K`            

תרשים 2

 

עקומות שוות תפוקה ו- RTS

אוסף כל הנקודות המייצגות הרכבי גורמי ייצור המניבים אותה תפוקה, יוצר קו שנקרא “עקומה שוות תפוקה”.
נתבונן בפונקציית הייצור `x=L*K` 
כל הרכבי גורמי הייצור הבאים נמצאים על אותה עקומה שוות תפוקה: (1,30), (2,15), (3,10), (5,6), (6,5), (10,3), (15,2), (30,1).
כל הסלים האלו מניבים 30 יחידות מוצר x.
לכל רמת תפוקה קיימת עקומה שוות תפוקה.
היות ורמת התפוקה היא משתנה רציף, קיימות אינסוף עקומות שוות תפוקה.

 

תוואי עקומות שוות תפוקה

עקומה שוות תפוקה יורדת משמאל לימין (שיפוע שלילי).
המשמעות היא שכדי לייצר כמות תפוקה כלשהי, על כל תוספת של 1 יח' מ-L, ניתן לוותר על כמות כלשהי של יחידות מ-K (תרשים 3).

 

תרשים 3

תוואי עקומות שוות תפוקה

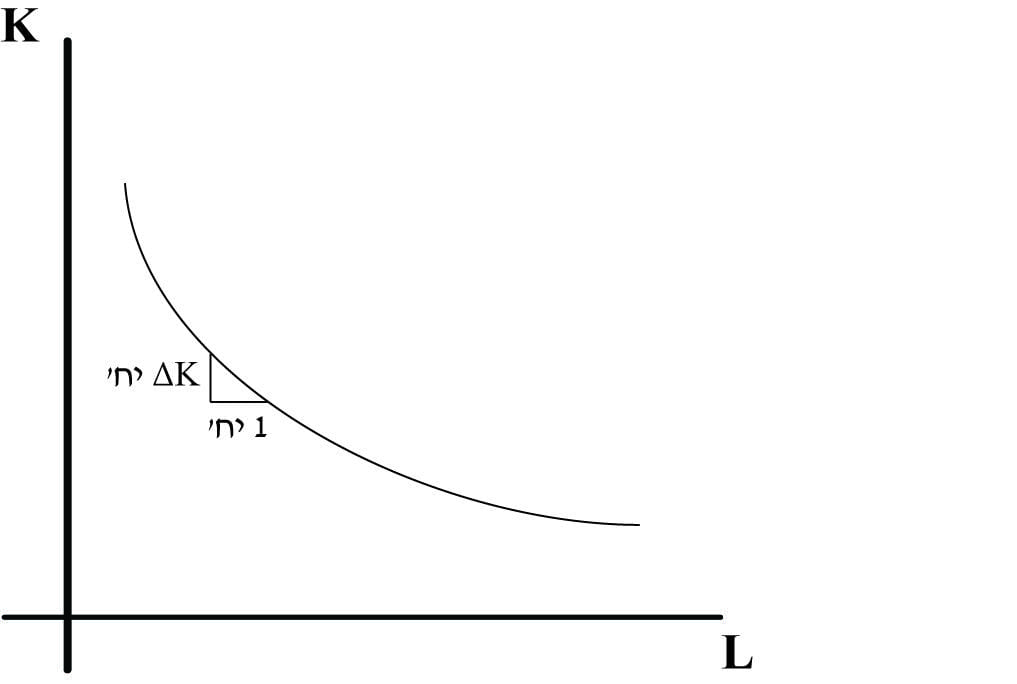
עקומה שוות תפוקה מתאפיינת בתכונת השיוויון הבאה:

התפוקה הנובעת מתוספת יחידה מ-L משתווה להפסד התפוקה שנובע מהוויתור הנדרש על כמות יחידות כלשהי מ- K.

את כמות היחידות מ- K שעלינו לוותר עליהן נסמן ∆K.

תוספת התפוקה שווה ל: 1 (יח' מ- L)·`MP_L`     ( `MP_L` – התפוקה השולית של L)

הפסד התפוקה שווה ל: ∆K (יח' מ- K)·`MP_K`  ( `MP_K` – התפוקה השולית של K)

השיוויון הנ”ל מוצג במשוואה 1.

משוואה 1: `MP_K*DeltaK=MP_L*1`

אם נשנה את סדר האיברים במשוואה 1 נקבל את משוואה 2.

 

משוואה 2: `(DeltaK)/1=(MP_(L))/(MP_K)`` `
( `(DeltaK)/1`  זהו יחס התפוקות השוליות)
( `(MP_(L))/(MP_K)`  זהו יחס התפוקות השוליות)
כלומר, הנגזרת של פונקציית עקומה שוות תפוקה בכל נקודה, שווה ליחס התפוקות השוליות באותה נקודה.

 

התייחסות יותר כללית

גידול התפוקה הנובע מתוספת של ∆L יחידות משתווה להפסד התפוקה הנובע מהוויתור הנדרש מ- K שנסמלו ∆K (תרשים 4). 

תרשים 4

גידול התפוקה הנובע מתוספת של 

 

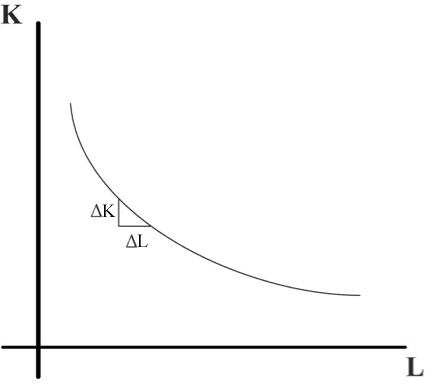
השיוויון מוצג במשוואה 3.
משוואה 3: `K*MP_K=L*MP_L`

אם נשנה את סדר האיברים במשוואה 3 נקבל את משוואה 4.

משוואה 4:  `(DeltaK)/(DeltaL)=(MP_(L))/(MP_K)` 

שימו לב: האיברים המתייחסים ל-L נמצאים במונה בצד אחד של המשוואה ובמכנה בצידה השני, וכך גם האיברים המתייחסים ל-K.

 

RTS – ר”ת של Rate of Technical Substitution

RTS הוא הכינוי לשיפוע עקומה שוות תפוקה.

בעברית מתייחסים למונח RTS כשיעור התחלופה השולי בייצור.

 

דוגמא לחישוב RTS של עקומה שוות תפוקה

פונקציית הייצור היא `x=L^2*K` . חשב את RTS בנקודה (1,1) [L=1,K=1].

 

פתרון

בכל נקודה על העקומה מתקיים היחס: `(DeltaK)/(DeltaL)=(MP_(L))/(MP_K)` (משוואה 4).

`(DeltaK)/(DeltaL)`  הוא שיפוע העקומה, RTS.

מהשוויון נוכל לחשב את RTS ע”י חישוב היחס `(MP_(L))/(MP_K)` .

חישוב `MP_L` :  `MP_L=(X_L)=2LK` (`X_L` – נגזרת ראשונה לפי L)

חישוב `MP_K` :  `MP_K=(X_K)=L^2` ( `X_K` – נגזרת ראשונה לפי K)

והתוצאה: RTS בנקודה (1,1) היא 2 `[(2LK)/L^2=(2K)/L=(2*1)/1=]`