בתורת היצרן נעסוק בעיקר בקשר שבין גורמי הייצור לתפוקה.
גורמי ייצור
נעסוק ב- 2 גורמי ייצור: עובדים והון.
- עובדים את מספר העובדים נסמל ב- `L` (L – קיצור של Labor).
- הון הון כולל בעיקר מכונות וציוד. אנו נתמקד במכונות.
את מספר המכונות נסמל ב- `K` (K- קיצור של Kapital מגרמנית.
באנגלית המילה Capital רשומה עם `C` ).
סל גורמי ייצור
להרכב כלשהו של 2 גורמי הייצור נקרא סל גורמי ייצור או בקיצור סל.
כל סל מכיל כמות כלשהי מ-L (לרבות 0) וכמות כלשהי מ-K (לרבות 0).
מישור גורמי ייצור (תרשים 1)
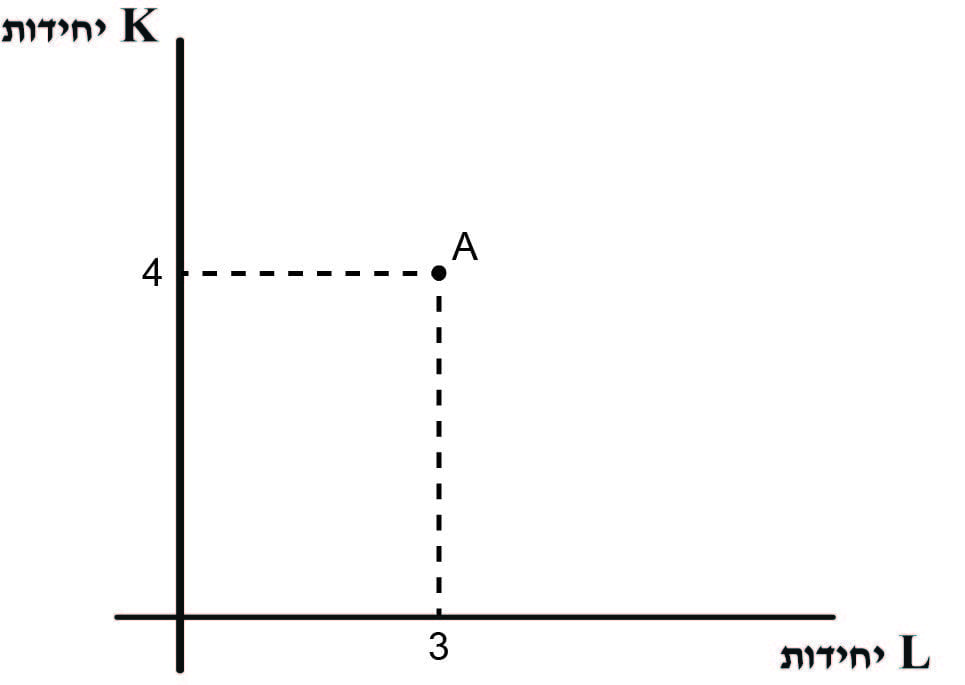
כל הרכב של גורמי ייצור מקבל ביטוי באמצעות נקודה במישור שציריו הם K ו- L.
נקודות הציון של הנקודה תואמות את הרכב הסל.
לדוגמא, בסל המיוצג ע”י הנקודה A בתרשים 1 יש 3 יחידות מגורם הייצור L ו- 4 יחידות מגורם הייצור K.
תרשים 1
סימול מחיר גורמי הייצור
`PL` – המחיר (עלות) של `L`
`PK` – המחיר (עלות) של `K`
עלות הסל
עלות הסל שנסמלה `TC` מתקבלת מהנוסחה: `TC=L*P_(L)+K*P_(K)` .
חישוב היקף התפוקה באמצעות פונקציית הייצור
את כמות יחידות הייצור נסמל ב- x.
כל סל מניב תפוקה כלשהי. התפוקה מחושבת באמצעות פונקציית הייצור של היצרן שמתייחסת לאותו מוצר.
אם למשל פונקציית הייצור היא `x = L*K` והרכב הסל הוא (10,3) [L=10,K=3],
אזי התפוקה תסתכם ב-30 יח' [=3*10] המוצר.
סימולים המתלווים לפונקציית הייצור (חזרה והשלמות) בתוספת פרשנות ומשמעות (x=x(L,K
פונקציית ייצור – `L` מייצג את מספר העובדים
`K` מייצג את מספר המכונות
`X_L` נגזרת ראשונה לפי L
`X_K` נגזרת ראשונה לפי K
`X_L_L` נגזרת ראשונה לפי L, נגזרת שנייה לפי L
`X_K_K` נגזרת ראשונה לפי K, נגזרת שנייה לפי K
`X_L_K` נגזרת ראשונה לפי L, נגזרת שנייה לפי K (הנגזרת הצולבת)
`X_K_L` נגזרת ראשונה לפי K, נגזרת שנייה לפי L (הנגזרת הצולבת)
`MP_L` תפוקה שולית של עבודה
`MP_K` תפוקה שולית של הון
עבודה – L
התפוקה השולית של עבודה נוקבת בתוספת התפוקה שנובעת מהעסקת עובד נוסף (כאשר כמות המכונות נשארת קבועה).
כאשר ניתנת פונקציית ייצור, אזי הנגזרת שלה לפי L (כאשר K קבוע בערך כלשהו) נוקבת בתפוקה השולית המתייחסת לכל ערך של L.
לדוגמא בפונקציית הייצור `x=L^2*k` התפוקה השולית של `L` היא `X_L=2LK` , לכל ערך של `K` . למשל, אם `K=20` התפוקה השולית של `L` היא `X_L = 40L` .
התפוקה השולית של העובד הראשון (1 = L) היא 40 יח' `(2*1*20=)` [L=1,K=20].
התפוקה השולית של העובד השני (2 = L) היא 80 יח‘ `(2*2*20=)` [L=2,K=20]., וכך הלאה.
מכונות – K
התפוקה השולית של מכונות נוקבת בתוספת התפוקה שנובעת מהפעלת מכונה נוספת (כאשר מספר העובדים נשאר קבוע).
בדוגמא שבה פונקציית הייצור היא `x=L^2*K` , התפוקה השולית של K היא `X_K=L^2` , לכל ערך של L.
לדוגמא, כאשר מס' העובדים הוא `L=10` , התפוקה השולית של כל מכונה נוספת היא 100 יח'.
הגידול במספר המכונות לא משפיע על התפוקה השולית שלהן – התפוקה השולית של מכונות בדוגמא זו לא תלויה במספר המכונות.
ייצור התפוקה במחיר הזול ביותר (הסל הנבחר)
כל רמת תפוקה ניתן לייצר באמצעות מספר רב של סלים.
אנו כמובן נעדיף את הסל הזול ביותר.
תשואה לגודל
התשואה לגודל בוחנת כיצד משפיע גידול בשיעור שווה ב-2 גורמי הייצור על שיעור הגידול בתפוקה.
לדוגמא, באיזה שיעור תגדל התפוקה אם נגדיל פי 2 את הכמות של כל אחד מגורמי הייצור בסל המקורי?
קיימות 3 אפשרויות:
שיעור הגידול בתפוקה שווה לשיעור הגידול בכמויות גורמי הייצור בסל.אפשרות זו מכונה: תשואה קבועה לגודל (תק”ל).
שיעור הגידול בתפוקה גדול משיעור הגידול בכמויות גורמי הייצור בסל.אפשרות זו מכונה: תשואה עולה לגודל (תע”ל).
שיעור הגידול בתפוקה קטן משיעור הגידול בכמויות של גורמי הייצור בסל.אפשרות זו מכונה: תשואה יורדת לגודל (תי”ל).
התשואה לגודל מושפעת מצורת פונקציית הייצור
צורת פונקציית הייצור קובעת את מגמת התשואה לגודל.
נציג 3 פונקציות שמניבות 3 תוצאות שונותף
- תשואה קבועה לגודל
כאשר פונקציית הייצור היא `x=sqrt(L)*sqrt(K)`, מתקבלת תשואה קבועה לגודל (תק”ל).
דוגמא
כאשר הרכב הסל הוא (4,9)[4=L9=K] מתקבלת תפוקה של 6 יח'`(sqrt(4)*sqrt(9)=)`
כאשר הרכב הסל מוכפל ל-(8,18) מתקבלת תפוקה של 12 יח' `(sqrt(8)*sqrt(18)=)`
התפוקה גדלה באותו שיעור שבו גדל כל אחד מגורמי הייצור.
בכל הרכב סל שנבחר נקבל תשואה קבועה לגודל - תשואה עולה לגודל
כאשר פונקציית הייצור היא `x=L*K` , מתקבלת תשואה עולה לגודל (תע”ל).
דוגמא
כאשר הרכב הסל הוא (1,1) מתקבלת תפוקה של 1 יח' `(1*1=)`
כאשר הרכב הסל מוכפל ל-(2,2) מתקבלת תפוקה של 4 יח' `(2*2=)` , פי 4.
כאשר הרכב הסל מוכפל שוב ל-(4,4) מתקבלת תפוקה של 16 יח'`(4*4=)` , פי 4.
בכל הרכב סל שנבחר, תמיד נקבל תשואה עולה לגודל - תשואה יורדת לגודל
כאשר פונקציית הייצור היא `x=sqrt(L)+sqrt(K)`, מתקבלת תשואה יורדת לגודל (תי”ל).
דוגמא
כאשר הרכב הסל הוא (1,4) מתקבלת תפוקה של 3 יח' `(sqrt(1)+sqrt(4)=)` .
כאשר הרכב הסל מוכפל ל- (2,8) מתקבלת תפוקה של 4.2 יח'`(sqrt(2)+sqrt(8)=)` , פי 1.4.
בכל הרכב סל שנבחר, תמיד נקבל תשואה יורדת לגודל