בפרק זה נעסוק במונופול הפועל בשוק אשר בו קיים סחר בינלאומי (יבוא/יצוא).
אנו נניח שהמונופול מוכר בשוק המקומי ויכול גם לייצא, אם זה כדאי לו מבחינה כלכלית.
באשר ליבוא נבחן מספר תרחישים.
תרחיש 1 – אין יבוא והמונופול יכול להפלות בין השוק המקומי והיצוא.
תרחיש 2 – אין יבוא והממשלה אוסרת על המונופול להפלות.
תרחיש 3 – הצרכנים בשוק המקומי יכולים לייבא ישירות.
תרחיש 4 – הצרכנים בשוק המקומי אינם יכולים לייבא אך המונופול יכול לייבא וגם להפלות.
הנחות נוספות
- בשוק הבינ”ל למוצר יש מחיר קבוע וידוע, שנכנה אותו: המחיר הבינלאומי.
- גם היצוא וגם היבוא נעשים במחיר הבינ”ל.
התייחסות ל-2 שווקים
בפרק זה נעסוק בשני שווקים.
- השוק המקומי.
- השוק הבינ”ל.
השוק הבינ”ל מבחינתנו הוא שוק הומוגני אחד.
סימולים
`D` – השוק המקומי (קיצור של Domestic)
`I` – השוק הבינ”ל (קיצור של International)
`P_D` – המחיר המקומי
`P_I` – המחיר הבינ”ל (כדי לפשט נתייחס למחיר במונחי ש”ח)
`Q_D` – הכמות שתימכר בשוק המקומי
`Q_I` – הכמות שתימכר בשוק הבינ”ל
`Q=Q_D+Q_I`
אין ייבוא והמונופול יכול להפלות – תרחיש 1
האפליה מתבטאת בכך שהמונופול יכול לדרוש מחיר שונה בכל אחד מהשווקים: המחיר בשוק המקומי יכול להיות שונה מאשר בשוק הבינ”ל, שם המחיר הוא כאמור המחיר הבינ”ל.
דוגמא 1
נתוני הייצוא המקומי הם כדלקמן:
פונקציות העלות: `TC(Q)= Q^2`
פונקציית הביקוש בשוק המקומי: `P_D=100-Q_D`
המחיר הבינ”ל: 30 ש”ח
הפתרון
פונקציית הרווח: `Pi=Q_D*P_D+Q_I*P_I-(Q_D+Q_I)^2`
במקום `P_D` , נציב: `[100-Q_D]`
במקום `P_I` , נציב: 30 ש”ח
ונקבל: `Pi=Q_D(100-Q_D)+Q_I*30-(Q_D+Q_I)^2=`
נפשט את הפונקציה ונקבל: `Pi=100Q_D-2Q_D^2+30Q_I-Q_I^2-2Q_DQ_I`
תזכורת מתמטית
נקודת הקיצון של פונקציה עם 2 משתנים, מתקבלת במקום שהנגזרת של כל אחד מהמשתנים היא 0.
QD ו- QI הם המשתנים.
נגזור לפי `Q_D` ונשווה ל-0. התוצאה: `100-4Q_D-2Q_I=0`
נגזור לפי `Q_I` ונשווה ל-0. התוצאה: `30-2Q_I-2Q_D=0`
מפתרון שתי המשוואות מתקבל: `Q_D=35` , `Q_I=-20` . התקבלה כמות שלילית בחו”ל.
לאור התוצאה, המונופול לא ייצא לשוק הבינ”ל, והוא ידאג למקסם את רווחיו בשוק המקומי.
הנתונים המתייחסים לשוק המקומי הם:
הרווח המקסימלי מתקבל בכמות שבה מתקיים השוויון MC=MR.
דוגמא 2
הדוגמא מתבססת על נתוני דוגמא 1 מלבד העובדה שהמחיר הבינ”ל עלה מ-30 ל-70 ש”ח.
פתרון
פונקציית הרווח היא: `Pi=Q_D(100-Q_D)+Q_I*70-(Q_D+Q_I)^2`
(כמו בדוגמא 1 רק שעבור המחיר הבינ”ל הצבנו 70 במקום 30).
נפשט את הפונקציה ונקבל: `Pi=100Q_D-2Q_D^2+70Q_I-Q_I^2-2Q_DQ_I`
נגזור לפי `Q_D` ונשווה ל-0. התוצאה: `100-4Q_D-2Q_I=0`
נגזור לפי `Q_I` ונשווה ל-0. התוצאה: `70-2Q_I-2Q_D=0`
מפתרון המשוואות מתקבל:
מסקנות
המונופול ימכור 15 יח' בשוק המקומי במחיר של 85 ש”ח, וייצא 20 יח' לשוק הבינ”ל במחיר שווה ערך ל- 70 ש”ח.
אין ייבוא אך חל איסור להפלות – תרחיש 2
כשהמונופול לא יכול להפלות, המחיר המקומי זהה למחיר הבינ”ל.
דוגמא 3
דוגמא 3 מתייחסת לנתוני דוגמא 2.
2 הערות מקדימות
- כאשר רק המחיר הבינ”ל בתוקף, פונקציית הרווח הופכת להיות פונקציה של משתנה אחד כפי שנראה מיד.
- פונקציית הביקוש המקומי היא: `P_D=100-Q_D` . היות ו- P`D=PI=70` ש”ח, אזי: `QD=30` יח' .
הפתרון
פונקציית הרווח: `Pi=Q_D*P_I+Q_I*P_I-(Q_D+Q_I)^2=30*70+Q_I*70-(30+Q_I)^2`
נפשט ונקבל: `Pi=1200+10Q_I-Q_I^2`
התוצאה:
רווח המונופול: 1225 ש”ח `(=1200+50-25)`
ריכוז התוצאות בדוגמאות 1-3
- דוגמא 1 – כאשר המחיר הבינ”ל עמד על 30 ש”ח והמונופול יכול היה להפלות, הוא העדיף למכור רק בשוק המקומי והרוויח 1,250 ש”ח.
- דוגמא 2 – כאשר המחיר הבינ”ל עמד על 70 ש”ח והמחיר המקומי על 85 ש”ח, המונופול היה יכול להפלות, המונופול מכר בשני השווקים במחירים שונים, והרווח גדל ל-1,450 ש”ח.
- דוגמא 3 – כאשר המחיר הבינ”ל עמד על 70 ש”ח אך המונופול לא היה יכול להפלות, רווח המונופול ירד ל- 1,225 ש”ח.
- (המונופול הפסיד את תוספת המחיר בסך 15 ש”ח שיכל לקבל בשוק המקומי אלמלא האיסור על הפליית מחירים).
הצרכנים בשוק המקומי יכולים לייבא – תרחיש 3
כאשר הצרכנים בשוק המקומי יכולים לייבא, המונופול לא יכול להפלות במחירים, והמחיר בשוק המקומי יהיה המחיר הבינ”ל (כולל מכס).
במצב זה, הפירמה המקומית אינה ב”מעמד” של מונופול.
הצרכנים בשוק המקומי אינם יכולים לייבא, אך המונופול יכול לייבא וגם להפלות – תרחיש 4
יכולת המונופול לייבא מחד ולייצא מאידך גורמים לשינויים בתוואי של עקומות MC ו-MR.
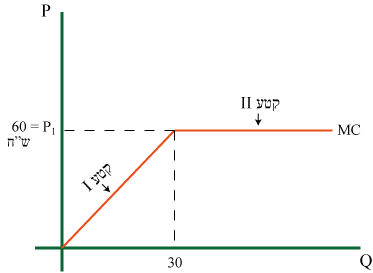
עקומת MC לא יכולה לעלות על PI (תרשים 27).
הסבר: מעל PI למונופול עדיף לייבא ולמכור בשוק המקומי מאשר לייצר בעצמו.
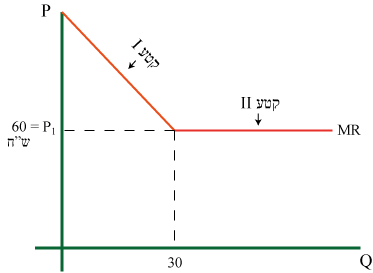
עקומת MR לא יכולה לרדת מ- PI (תרשים 28).
הסבר: כשהמחיר בשוק המקומי יורד מתחת ל- PI, למונופול עדיף לייצא ולמכור בשוק הבינ”ל.
תרשים 27 – תוואי עקומת MC תרשים 28 – תוואי עקומת MR
תוואי עקומת MC (תרשים 27)
העקומה מכילה 2 קטעים.
- קטע I – `MC` עולה עד לכמות שבה `MC=P_I` (בנתוני הדוגמא הכמות היא:30, ולכן יח' 2Q=60 ).
- קטע II – `MC=P_I` המונופול יכול לרכוש כל יחידה במחיר `P_I` .
לנקודת החיבור בין 2 הקטעים נקרא הברך של MC.
תוואי עקומת MR (תרשים 28)
העקומה מכילה 2 קטעים.
- קטע I – `MR` יורדת עד לכמות שבה `MR=P_I` (בנתוני הדוגמא הכמות היא: 20 יח', 100-2Q=60).
- קטע II – `MR=P_I` המונופול יכול למכור כל יחידה ב-`P_I` .
לנקודת החיבור בין 2 הקטעים נקרא הברך של MR.
סך הייצור וחלוקתו בין שוק מקומי וייצוא
נבחין בין 2 מצבים:
מצב I – הברך של MR נמצאת משמאל לזו של MC.
מצב II – הברך של MR נמצאת מימין לזו של MC.
מצב I (תרשים 29)
נתייחס לדוגמא שנתוניה הם:
פונקציית עלות הייצור: `TC=Q^2`
פונקציית הביקוש: `P_D=80-Q_D`
המחיר הבינ”ל: `P_I=60` ש”ח (נזכיר כי אנחנו מדברים על שווי המחיר הבינ”ל בש”ח)
תרשים 29
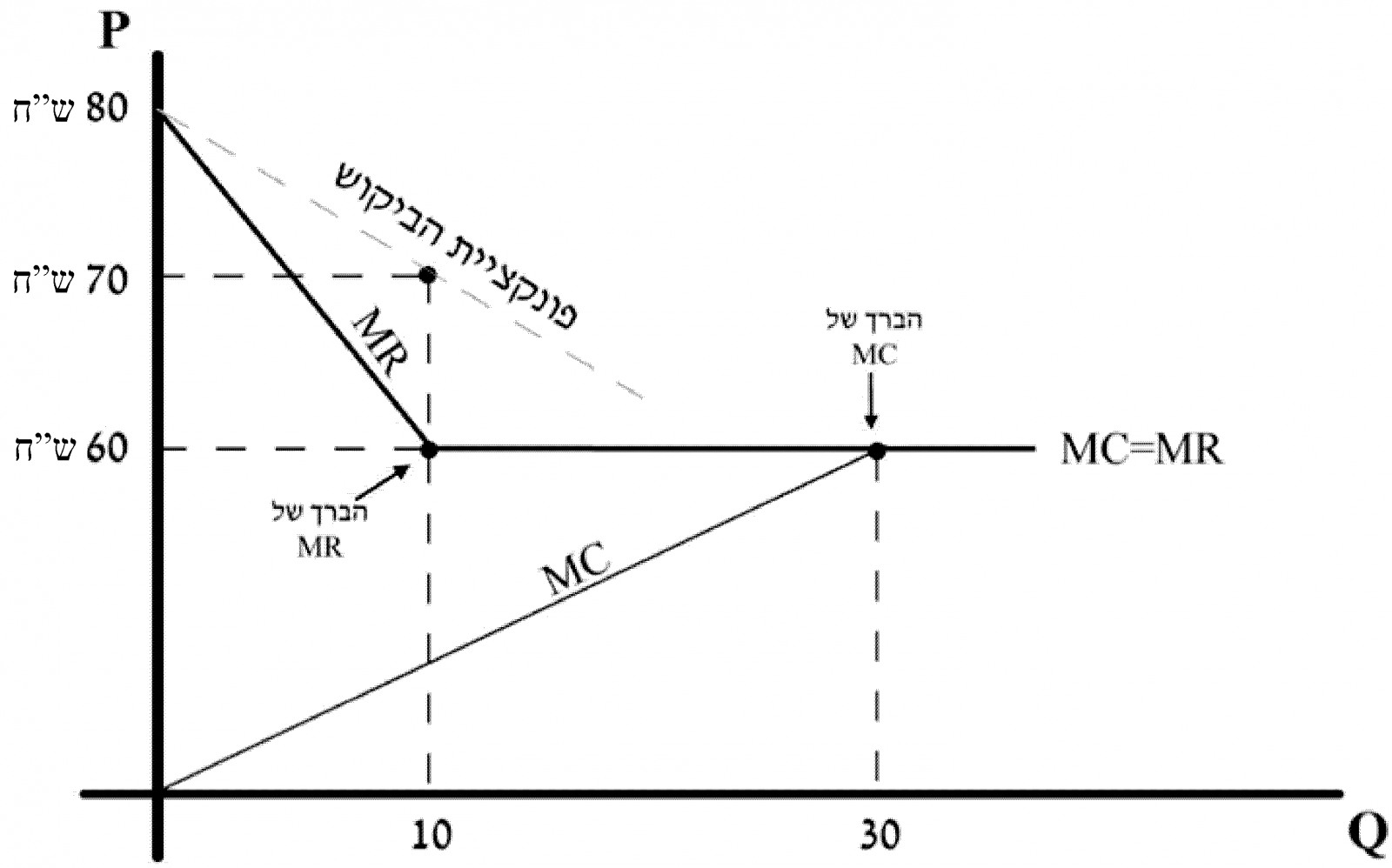
במצב I : הברך של MR מתקבלת בכמות של 10 יח' `[80-2Q=60]` `(P_I=60)`
הברך של MC מתקבלת בכמות של 30 יח' `[2Q=60]` `(P_I=60)`
במצב זה המונופול ייצר 30 יח'.
מתוכן הוא ימכור:
בשוק המקומי: 10 יח' במחיר של 70 ש”ח `(=P_D=80-10)`
יצוא לשוק הבינ”ל: 20 יח' במחיר של 60 ש”ח.
במצב I המונופול לא ייבא כלל.
פרשנות
- מכירה של כל יחידה נוספת בשוק המקומי מעבר ל- 10 יח' תוסיף לפדיון פחות ממכירה בחו”ל.
- לא כדאי למונופול לייצא מעבר ל-20 יח' שכן התמורה על כל יחידה נוספת תשתווה לעלות שלה או תהיה פחותה מהעלות.
מצב II (תרשים 30)
נתייחס לדוגמא שנתוניה הם:
- פונקציית עלות הייצור: `TC=Q^2`
- פונקציית הביקוש: `P_D=80-Q_D`
- המחיר הבינ”ל: `20=P_I`
תרשים 30
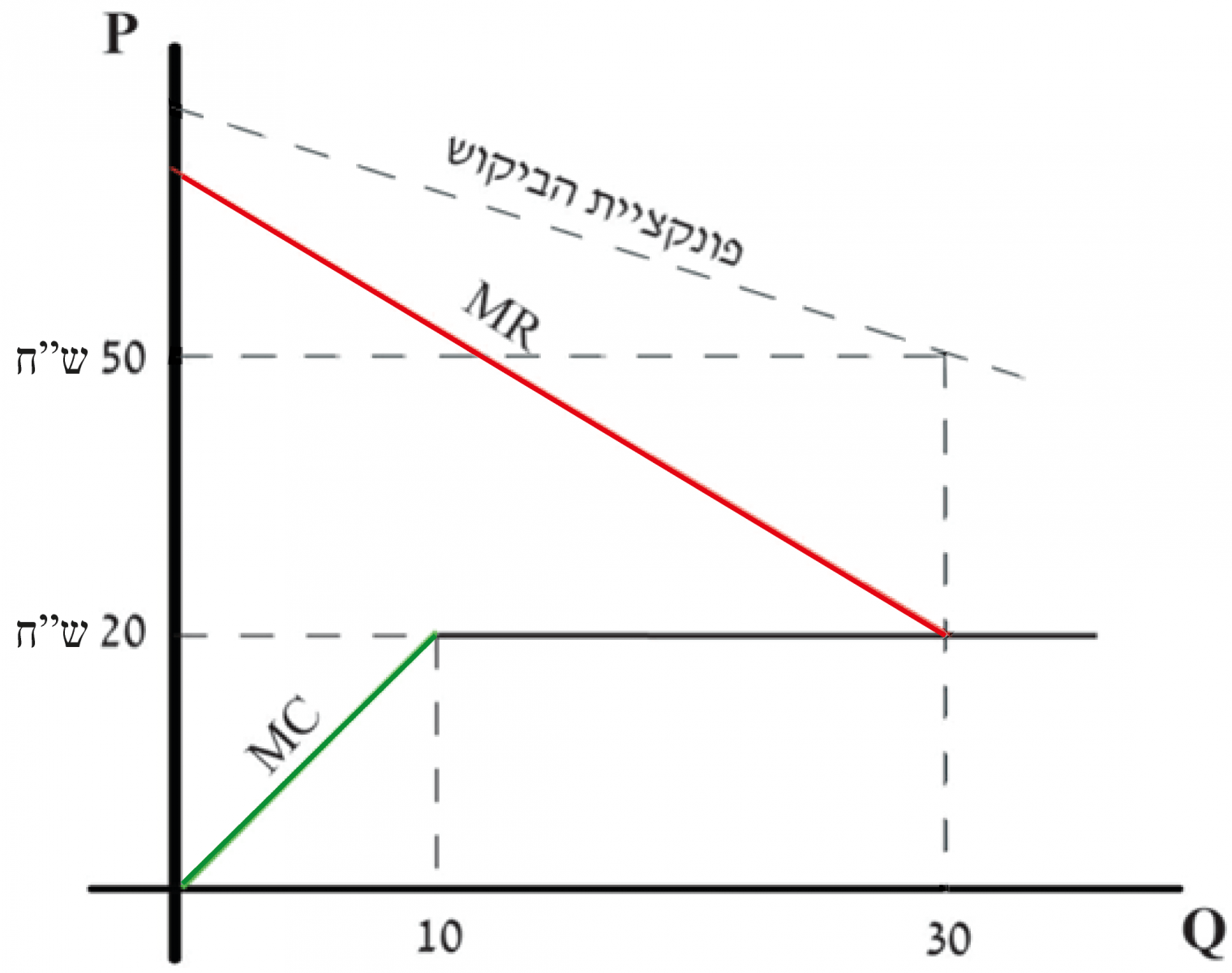
במצב II :
הברך של MR מתקבלת בכמות של 30 יח' `[MR=80-2Q),(P_I=20)quad=gtquad(80-2Q=20)]` – בנקודת המפגש עם המחיר הבינ”ל.
הברך של MC מתקבלת בכמות של 10 יח' `[MC=2Q),(P_I=20)quad=gtquad(2Q=20)]`
במצב זה המונופול ייצר 10 יח' בעצמו, וייבא עוד 20 יח'.
את כל היחידות הוא ימכור בשוק המקומי במחיר של 50 ש”ח `[(P_D=(80-Q_D]` .
במצב II המונופול לא ייצא כלל.
פרשנות
תוספת הפדיון בשוק המקומי מכל יחידה שמעל 30 יחידות תהיה קטנה מ- 20 ש”ח בעוד שעלותה היא 20 ש”ח, שכן יש צורך לייבאה (ייצור עצמי יעלה יותר מ- 20 ש”ח וברור שלא כדאי).