נניח שבענף הפועל בתנאי תחרות ישנן 4 פירמות זהות לחלוטין:
פונקציית הייצור של כל פירמה היא `TC=q^2+25`
עקומת הביקוש של הענף היא `P=120-Q`
`q` = תפוקת הפירמה
`P` = מחיר המוצר
`Q` = הביקוש הענפי
בנקודת שיווי משקל של הענף צריכות להתקיים 3 משוואות שבהן 3 משתנים (נעלמים) שהם: P , q, Q.
המשוואות הן:
|
משוואה 1: `P = 2_q` |
(שוויון בין MC ל- P ברמת הפירמה). |
|
משוואה 2: `Q = 120 – P` |
(נקודת שיווי משקל נמצאת על עקומת הביקוש הענפי). |
|
משוואה 3: `Q = 4_q` |
(סה”כ הביקוש הענפי צריך להשתוות לתפוקת 4 הפירמות). |
פתרון המשוואות
נציב את משוואות 1 ו- 3 במשוואה 2 (במקום P ו- Q) ונקבל: `4q=120-2q` .
תוצאת המשתנים הם:
20 = q יח' (ע”פ משוואה 2)
40 = P ש”ח (ע”פ משוואה 1)
80 = Q יח' (ע”פ משוואה 3)
הרווח של כל פירמה הוא: ש”ח`q*P-TC=20*40-(400+25)=375`
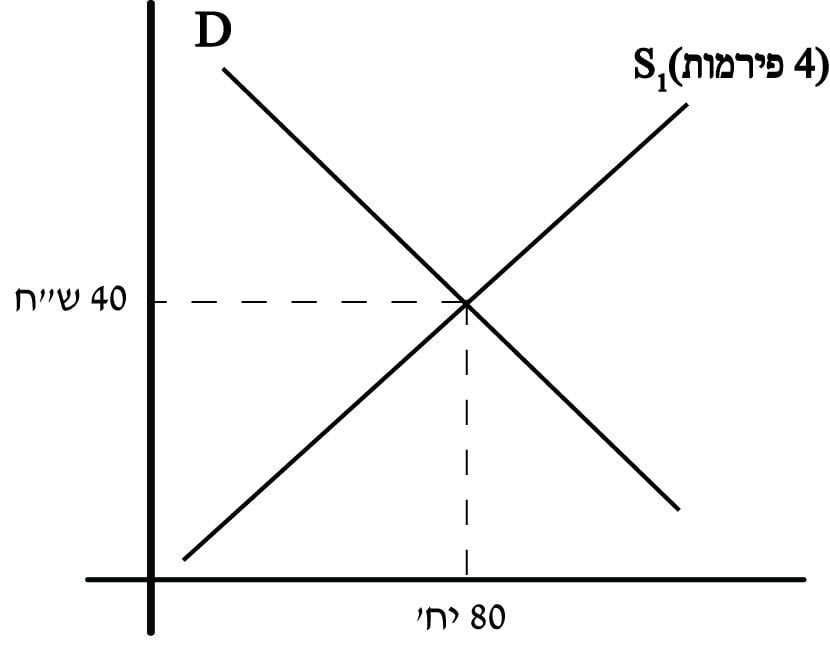
תרשים 18 מציג את נקודת שווי המשקל.
תרשים 18 שיווי משקל ענפי
רווח חיובי מעודד פירמות נוספות להיכנס לענף.
נניח שהתווספו עוד 6 פירמות הזהות לפירמות הקיימות.
בענף תתקבל נקודת שיווי משקל חדשה שבה מתקיימות 3 משוואות עם 3 משתנים (נעלמים):
|
משוואה 1: `P = 2_q` |
אין שינוי ברמת הפירמה – P = MC. |
|
משוואה 2: `Q = 120 – P` |
אין שינוי בעקומת הביקוש הענפי. |
|
משוואה 3: `Q = 10_q` |
סה”כ הביקוש הענפי צריך להשתוות לתפוקת 10 הפירמות. |
נציב במשוואה 2 : `10_q = 120 – 2_q`
פתרון המשוואות מניב את התוצאות הבאות:
במועד א' (4 פירמות)
במועד ב' (10 פירמות)
הרווח לפירמה: ש”ח `q*P-TC=10*20-(100+25)=75`
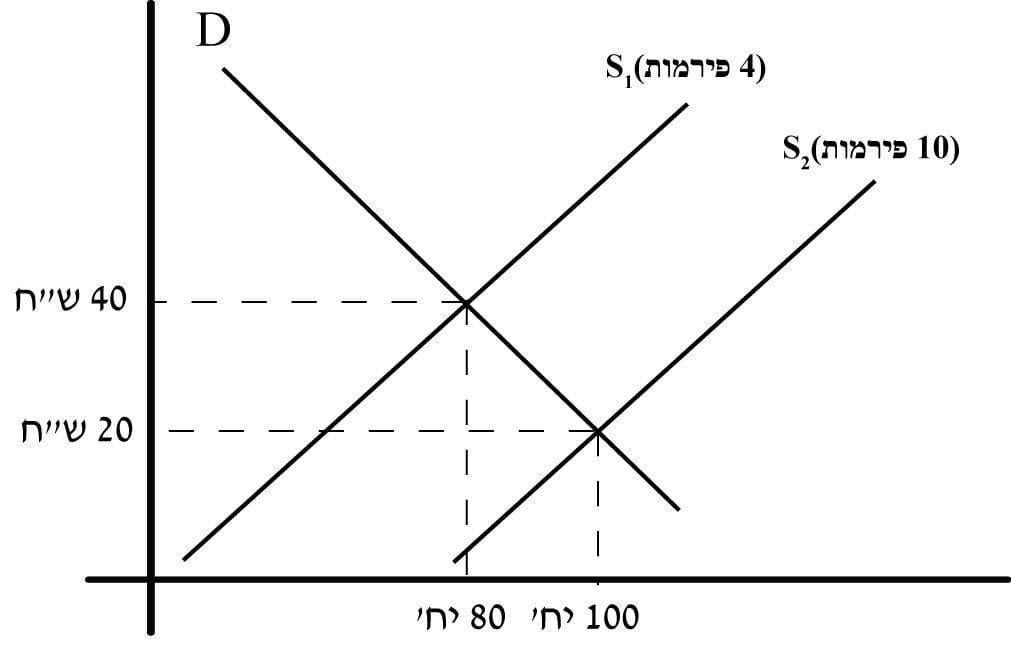
נקודה b בתרשים 19 מציגה את נקודת שיווי המשקל החדשה.
תרשים 19 –שיווי משקל ענפי
כמות הפירמות שתצטרפנה לענף
פירמות תמשכנה להיכנס לענף עד שהרווח לפירמה ירד ל- 0.
בתרחיש כזה, בנקודת שיווי המשקל בענף מתקיימות 4 משוואות עם 4 נעלמים שהן:
|
1. |
`P = 2_q` |
אין שינוי ברמת הפירמה |
|
2. |
`Q=120 – P` |
אין שינוי בעקומת הביקוש הענפי |
|
3. |
`Q=n*q` |
n – מספר הפירמות בענף |
|
4. |
`Pq-(q^2+25)=0` |
שוויון בין הפדיון להוצאות ברמת הפירמה |
פתרון
נציב את משוואה 1 ב-4 (במקום P) ונקבל `2q*q-(q^2+25)=0`
והתוצאה `q=5` .
Q = 110 יח'
n = 22 פירמות
פתרון שאר המשוואות מניב את התוצאות הבאות:
הרווח לפירמה: 0 ש”ח `q*P-TC=5*10-(25+25)=`
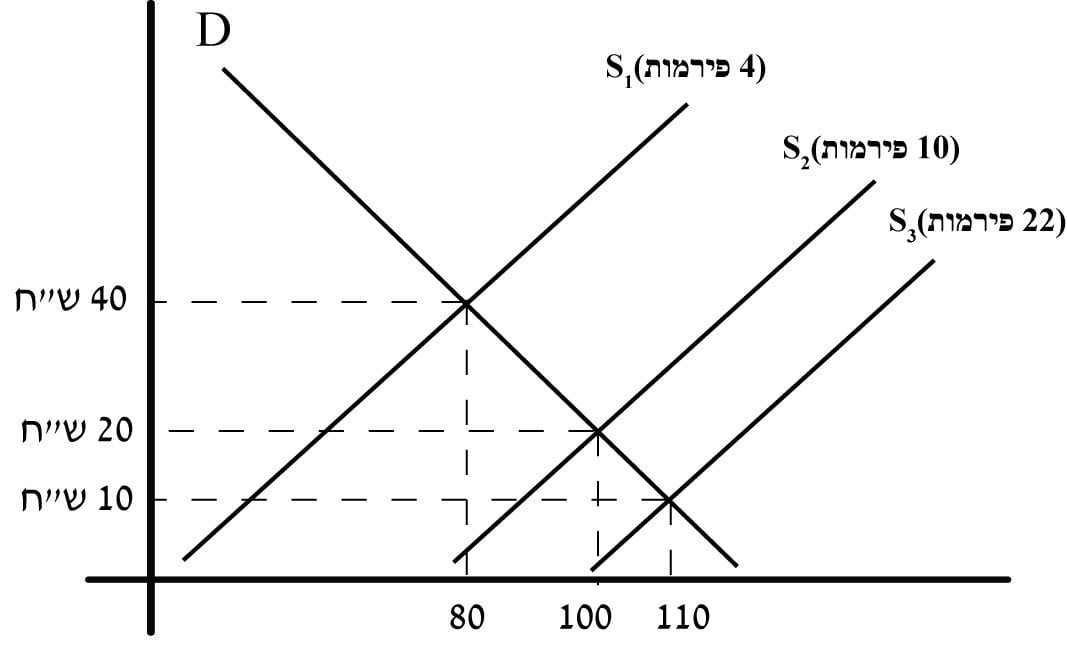
נקודה c בתרשים 20 מציגה את נקודת שיווי המשקל כאשר בשוק קיימות 22 פירמות.
תרשים 20– שיווי משקל ענפי