פונקציה לינארית
עקומת אנגל
צורת פונקציית הביקוש היא :
`x={(0 if alpha/betaP_(y_(0)<P_(x))),(0…I_(0)/P_(x) if alpha/betaP_(y_(0))=P_(x)),(I_(0)/P_(x) if alpha/betaP_(y_(0))>P_(x)):}`
צורת פונקציית אנגל היא :
`x={(0 if alpha/betaP_(y_(0)<P_(x_(0)))),(0…I/P_(x_(0)) if alpha/betaP_(y_(0))=P_(x_(0))),(I/P_(x_(0)) if alpha/betaP_(y_(0))>P_(x_(0))):}`
`- P_(x)` הופך לנתון `P_(x_(0))`
`- I_(0)` הופך למשתנה (I)
תוואי עקומת אנגל
מכל שורה בפונקציית אנגל מתקבל מתווה שונה.
כל שורה בפונקציית אנגל היא תרחיש אפשרי:
מתווה 1 מתקבל בתרחיש שבו `P_(x_(0))` נחשב יקר `[alpha/betaP_(y_(0))<P_(x_(0))]`
מתווה 2 מתקבל בתרחיש שבו `P_(x_(0))` נחשב גבולי `[alpha/betaP_(y_(0))=P_(x_(0))]`
מתווה 3 מתקבל בתרחיש שבו `P_(x_(0))` נחשב זול `[alpha/betaP_(y_(0))>P_(x_(0))]`
נציג את המתווה בכל תרחיש באמצעות דוגמה שבה נתוני `P_(x_(0))` ו-`P_(y_(0))` תואמים לתרחיש.
בכל הדוגמאות α=3, β=2 ו-I הוא המשתנה.
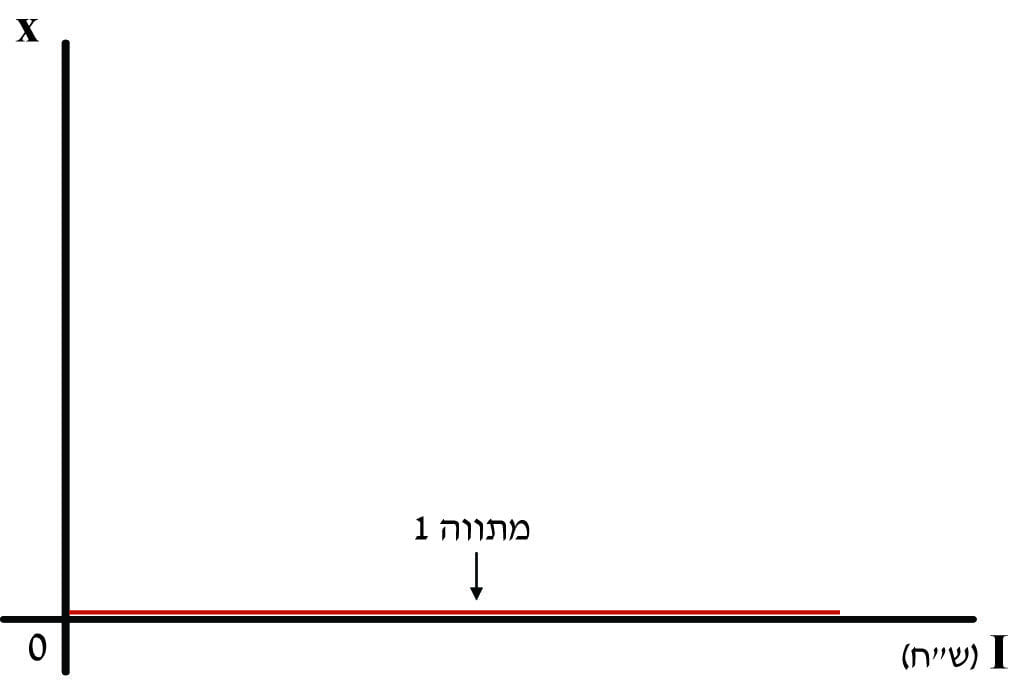
מתווה 1 מתקבל כאשר `P_(x_(0))` נחשב ליקר (תרשים 22)
`P_(x_(0))=20`
`P_(y_(0))=10`
`[alpha/betaP_(y_(0))=15]`
במתווה 1 הביקוש ל- x הוא 0.
בכל רמת הכנסה קונים רק מוצרי y.
במתווה 1, עקומת אנגל מתחילה בראשית הצירים וחופפת לציר האופקי.
תרשים 22
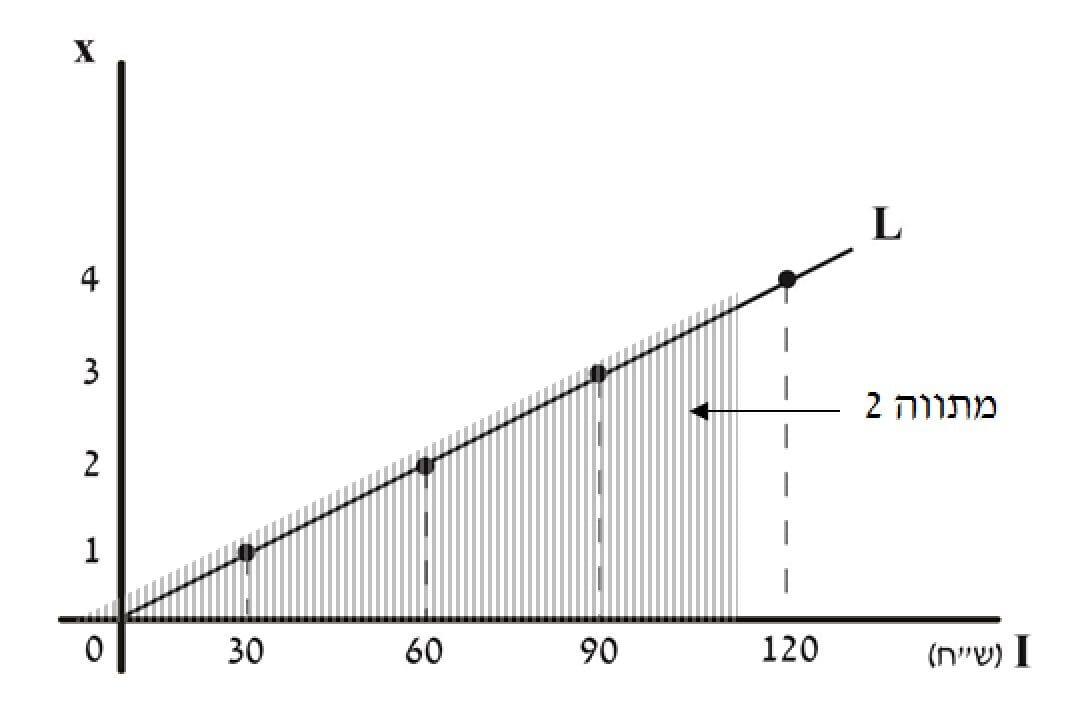
מתווה 2 מתקבל כאשר `P_(x_(0))` גבולי (תרשים 23)
`P_(x_(0))=30`
במתווה 2 בכל רמת הכנסה הביקוש ל- x נע בין 0 ל-`I/P_(x_(0))`
כאשר I = 30, ה-x יכול לנוע בין 0 ל-1 `30/30`
כאשר I = 60, ה-x יכול לנוע בין 0 ל- 2 `60/30`
גידול של פי n ב-I, מגדיל פי n את התחום ש-x יכול להגיע.
תוואי עקומת אנגל בתרחיש זה הוא רצף כל הקווים האנכיים שמתחילים בציר ה- x ומסתיימים בקו L. למעשה אם היינו משרטטים את כל הקווים האפשריים הם היו נוגעים זה בזה ויוצרים גוש שחור בצורת משולש שקודקודיו הם: 0, נקודה כלשהי על ציר ה-I ונקודה מעליו על קו L.
הערה: הקו האלכסוני L אינו חֶלֶק מעקומת אנגל. הוא נועד רק לְתחוֹם את הערך המקסימלי ש-x יכול לקבל בכל רמת הכנסה, ונוסחתו `x=I/P_(x_(0))`
תרשים 23
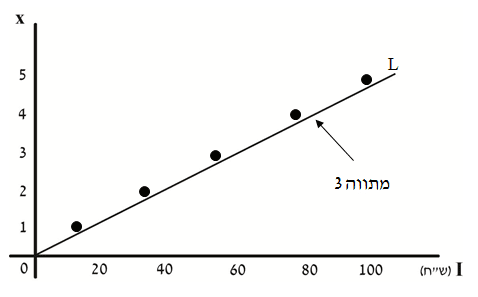
מתווה 3 מתקבל כאשר `P_(x_(0))` נחשב זול (תרשים 24)
התרשים מתבסס על הנתונים הבאים :
`P_(x_(0))=20`
`P_(y_(0))=20`
`[alpha/betaP_(y_(0))=30]`
במתווה 3 הביקוש ל- x בכל רמת הכנסה הוא `I/20` .
מתווה 3 הוא למעשה קו L (שנוסחתו `I/20` ) בתרשים 24.
גידול של פי n ב-I, מגדיל פי n את הביקוש ל- x.
תרשים 24
פרשנות
- במתווה 3 בעקבות הגידול בהכנסה, עקומת הביקוש זזה ימינה בכל רמת מחיר באותו שיעור שבו גדלה ההכנסה. תוואי עקומת הביקוש כאשר x נחשב כזול יורדת משמאל לימין וגמישותה 1.
- כל אחד מ- 3 המתווים מהווה עקומת אנגל בפני עצמה. התוואים אינם קטעים בעקומת אנגל אחת כלשהי.
עקומת הביקוש הצולב
צורת פונקציית הביקוש היא :
צורת פונקציית המחיר הצולב היא :
`x={(0 if P_(y)<P_(x_(0))beta/alpha), (0…I_(0)/P_(x_(0)) if P_(y)=P_(x_(0))beta/alpha), (I/P_(x_(0)) if P_(y)>P_(x_(0))beta/alpha):}`
כדי להציג את פונקציית המחיר הצולב, ארגנו בצורה שונה את היחס שבין `P_(x_(0))` ל-`alpha/betaP_(y)` על-ידי כך שבודדנו את Py (מבלי לשנות את יחסי אי השיוויון או השיוויון).
תוואי עקומת הביקוש הצולב (תרשים 25)
תוואי העקומה מחולק ל- 3 קטעים. כל קטע מתייחס לתרחיש שמותאם לאחת מהשורות בפונקציה.
`I_(0)` = 100
תרשים 25
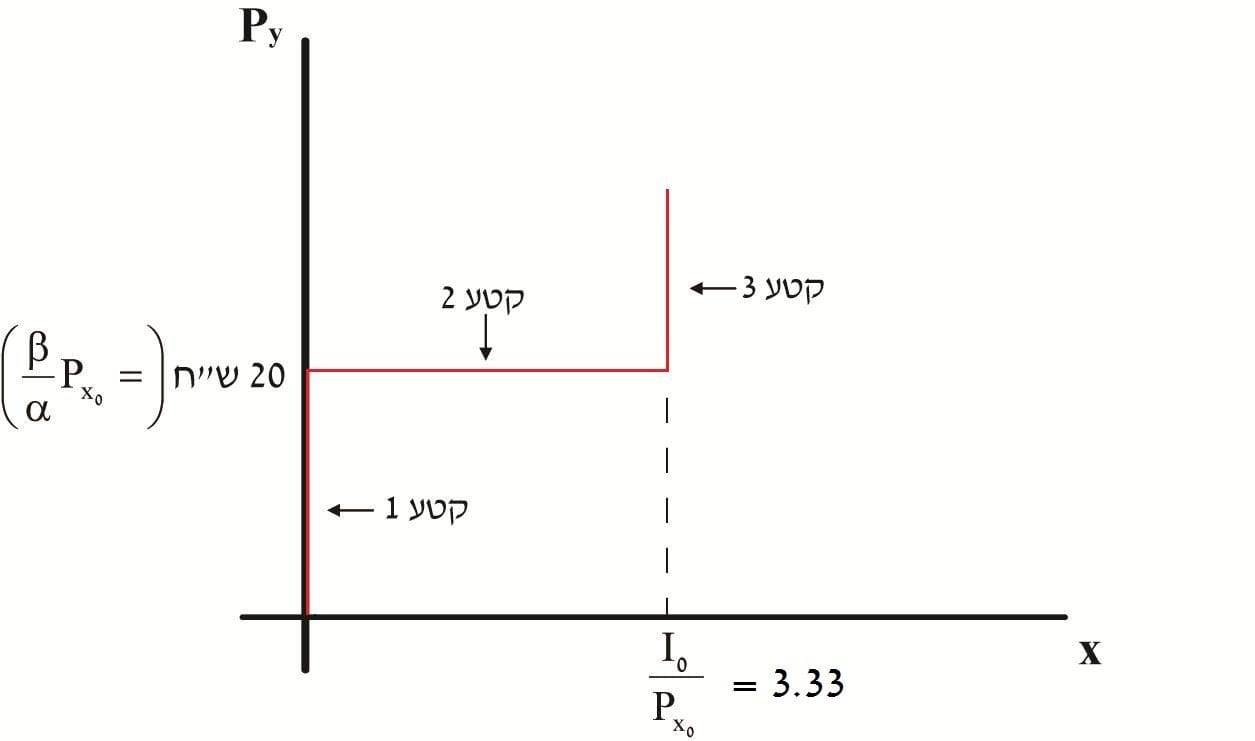
קטע 1 מתקבל כאשר Py נחשב זול (זול מ-`beta/alphaP_(x_(0))`). בנתוני הדוגמה, כאשר Py זול מ- 20 ש”ח.
בקטע זה הביקוש ל-x הוא 0 (קונים רק מוצרי y).
בקטע זה תוואי העקומה עולה מראשית הצירים לאורך ציר ה-y עד למחיר 20 ש”ח.
קטע 2 מתקבל כאשר Py נחשב גבולי. בנתוני הדוגמה, כאשר 20 ש”ח `P_(y_(0))=` `[P_(y)=beta/alphaP_(x_(0))]` , במחיר זה הכמות המבוקשת מ-x יכולה לנוע בין 0 ל-`I/P_(x_(0))` (=3.33 יחידות)
תוואי העקומה בקטע זה הוא קו אופקי בגובה 20 ש”ח. הקטע מתחיל ב-x=0 ומסתיים ב- x=3.33.
`3.33=[I/P_(x_(0))]`
קטע 3 מתקבל כאשר Py נחשב יקר. בנתוני הדוגמה, כאשר Py > 20 ש”ח
בקטע זה, שבו מחירי Py גבוהים מ- 20 ש”ח, הצרכן רוכש רק 3.33 יח' מ-x `[I_(0)/P_(x_(0))]` תוואי העקומה בקטע זה הוא אנכי. תחילתו בסוף קטע 2.
פרשנות
- כאשר המחיר של Py נחשב יקר, רוכשים רק מוצר x. הכמות:`[I_(0)/P_(x_(0))]` .
- כאשר המחיר של Py נחשב זול, רוכשים רק מוצר y ו- 0 מוצר x.
- כאשר המחיר של Py גבולי, הצרכן אדיש בין רכישת מוצר x ורכישת מוצר y.