פונקציית מינימום
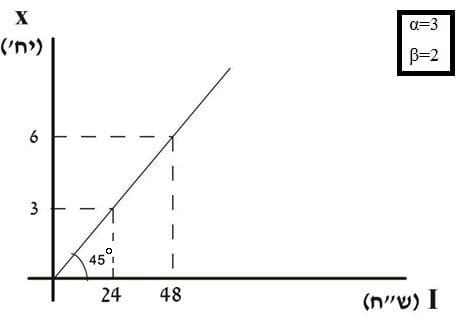
עקומת אנגל
צורת פונקציית הביקוש `x=(beta*I_(0))/(betaP_(x)+alphaP_(y_(o)))`
צורת פונקציית אנגל `x=(beta*I)/(betaP_(x_(0))+alphaP_(y_(0)))`
תוואי עקומת אנגל
`u(x,y)=min(3x,2y)`
תרשים 20
מאפייני התוואי
קו ישר העולה מראשית הצירים.
שיפועו: `(beta)/(betaP_(x_(0))+alphaP_(y_(o)))`. בנתוני הדוגמה: ⅛ או °45.
משמעות התוואי
השינוי בכמות המבוקשת מ- x פרופורציונלי לשינוי בהכנסה.
פרשנות
בעקבות הגידול בהכנסה, עקומת הביקוש זזה ימינה בכל רמת מחיר באותו שיעור שבו גדלה ההכנסה.
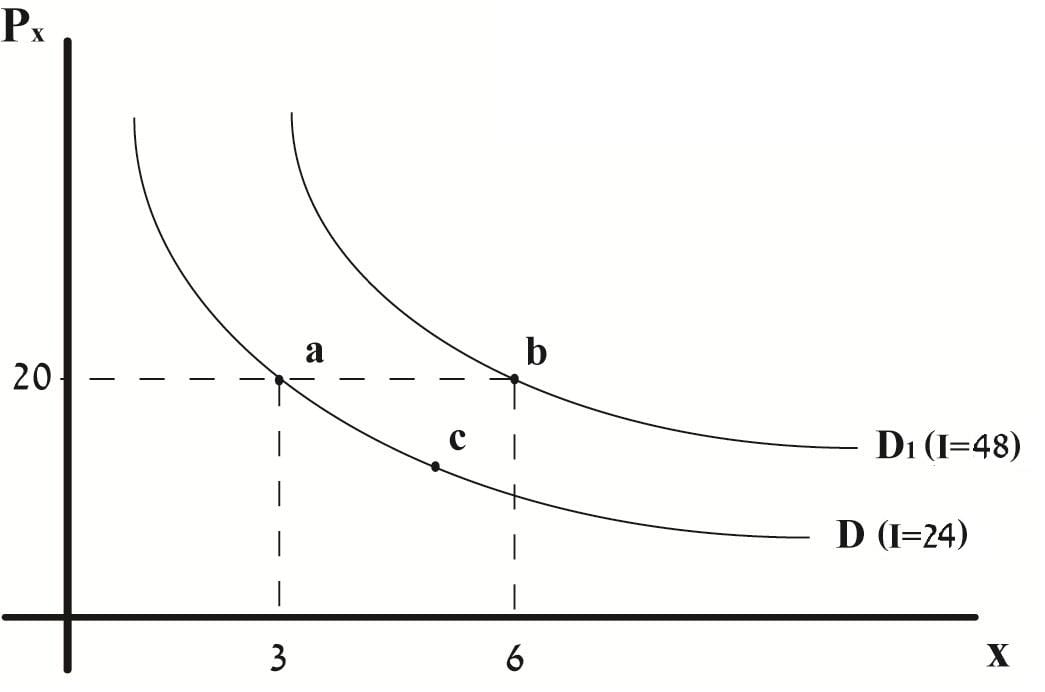
עקומת הביקוש הצולב
צורת פונקציית הביקוש היא: `(beta)/(betaP_(x)+alphaP_(y_(o)))`
צורת פונקציית הביקוש הצולב: `x=(beta*I_(0))/(betaP_(x_(0))+alphaP_(y))`
תוואי העקומה
תרשים 21 – עקומת הביקוש הצולב
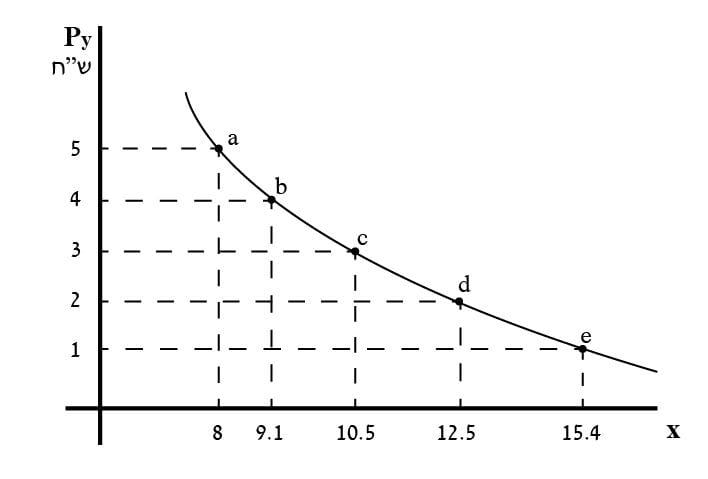
נתוני התוואי
הנקודות המשובצות על עקומת הביקוש הצולב בתרשים 21 חושבו תחילה על בסיס נתוני הדוגמה והוצבו בטבלה 6.
|
טבלה #6 |
||
|
סימול הנקודה |
`P_y` |
x |
|
a |
5 |
8 |
|
b |
4 |
9.1 |
|
c |
3 |
10.5 |
|
d |
2 |
12.5 |
|
e |
1 |
15.4 |